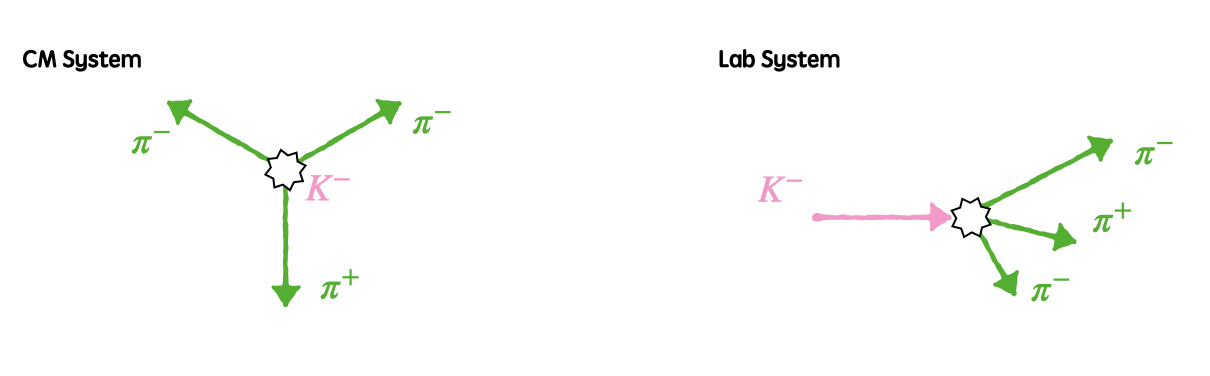3体崩壊(ハドロン)
二体反応まではArtemisの独自クラスTArtParticleにて簡単に計算することができますが、三体崩壊については少し複雑になります。
ここでは三体崩壊を自分たちで計算してみましょう。
想定する状況は以下の通りです。
二体反応(ハドロン)の時と同様に $K^{-}$を1 GeVまで加速した状態で飛行中に崩壊するという状況です。 二体崩壊と三体崩壊の異なる点は、重心系においても放出粒子のエネルギーが連続的なことです。 とはいえ崩壊によって生成される3つの粒子のうち2つの粒子を複合核のように扱って二体崩壊を計算したのちに、複合核の崩壊を考えればこれまでと近い形で計算できます。 このチュートリアルでは $K^{-} \rightarrow \pi^{-} + \pi^{-} + \pi^{+}$を計算しますが、これから計算過程の説明をしやすくするために崩壊粒子を以下のようにラベル付けします。
- 粒子1 : $\pi^{-} \rightarrow p_{1}^{\mu} = \left(E_{1},\,\vec{P_{1}}\right), \quad g_{\mu\nu}p_{1}^{\mu}p_{1}^{\nu} = \left(m_{1}\right)^{2}$
- 粒子2 : $\pi^{+} \rightarrow p_{2}^{\mu} = \left(E_{2},\,\vec{P_{2}}\right), \quad g_{\mu\nu}p_{2}^{\mu}p_{2}^{\nu} = \left(m_{2}\right)^{2}$
- 粒子3 : $\pi^{-} \rightarrow p_{3}^{\mu} = \left(E_{3},\,\vec{P_{3}}\right), \quad g_{\mu\nu}p_{3}^{\mu}p_{3}^{\nu} = \left(m_{3}\right)^{2}$
念の為グローバル変数を再定義します。
artemis [0] TDatabasePDG* gPDGMassTable = new TDatabasePDG();まずはよく使う変数を宣言します。
artemis [0] const Double_t m_Km = gPDGMassTable->GetParticle("K-")->Mass()*1000.;
artemis [1] const Double_t m_pim = gPDGMassTable->GetParticle("pi-")->Mass()*1000.;
artemis [2] const Double_t m_pip = gPDGMassTable->GetParticle("pi+")->Mass()*1000.;そして、ビーム粒子を宣言します。
artemis [3] TArtParticle *Km_S1CM = new TArtParticle();
artemis [4] Km_S1CM->SetXYZM(0,0,1000.,gPDGMassTable->GetParticle("K-")->Mass()*1000.);今回の二体崩壊計算を2回行うため考えてる系については慎重に考えないといけません。
よって上記の変数のように
$K^{-}$の運動速度と同様に運動する慣性系(
$K^{-}$にとって重心系)をS1CMと書いておきます。
次に複合核と1つの粒子の崩壊について考えていきます。
ここでは複合核を粒子2+粒子3とします。
そして質量などのラベルは
$m_{23}$のようにします。
artemis [5] const TVector3 VecSLab = Km_S1CM->BoostVector();
artemis [6] const Double_t M12_Min = m_pim + m_pip;
artemis [7] const Double_t M12_Max = m_Km - m_pim;
artemis [8] const Double_t M23_S1CM = gRandom->Uniform(M12_Min, M12_Max);
artemis [9] const Double_t P23_S1CM_Nume1 = TMath::Power(m_Km, 2) - TMath::Power(M23_S1CM+m_pim, 2);
artemis [10] const Double_t P23_S1CM_Nume2 = TMath::Power(m_Km, 2) - TMath::Power(M23_S1CM-m_pim, 2);
artemis [11] const Double_t P23_S1CM = TMath::Sqrt(P23_S1CM_Nume1*P23_S1CM_Nume2)/(2.*m_Km);上記のコマンドにおいて最初の行は最後に実験室系にBoostするときに使用します。 二行目からは崩壊後に生成される複合核と粒子1の4元ベクトルを計算しています。 複合核の取りうる不変質量の範囲ですが、以下のような条件になります。
$$ m_1 + m_2 \le m_{23} \le M -m_3 $$$M$は $K^{-}$の不変質量です。 この条件で複合核の不変質量を乱数で振って生成し、エネルギー・運動量を計算します。 運動量を計算できたあとは複合核と粒子3の4元ベクトルをセットし、複合核の崩壊を計算していきます。
artemis [12] TArtParticle *Km_pim1_S1CM = new TArtParticle();
artemis [13] TArtParticle *Km_M0_S1CM = new TArtParticle();
artemis [14] Km_pim1_S1CM->SetPxPyPzE( 0., 0.,P23_S1CM, TMath::Sqrt(m_pim*m_pim+P23_S1CM*P23_S1CM) );
artemis [15] Km_M0_S1CM->SetXYZM(0., 0., -P23_S1CM, M23_S1CM);上記では運動量はZ方向のみに振り分けていますが、実際は当方的に放出されるはずです。 そのため以下のようにして角度を振ったのちに崩壊の計算を行います。
artemis [16] const Double_t Ksitheta = TMath::ACos(2 * gRandom->Uniform() - 1.);
artemis [17] const Double_t Ksiphi = gRandom->Uniform(0.,2.*TMath::Pi());
artemis [18] Km_pim1_S1CM->RotateY(Ksitheta);
artemis [19] Km_pim1_S1CM->RotateZ(Ksiphi);
artemis [20] Km_M0_S1CM->RotateY(Ksitheta);
artemis [21] Km_M0_S1CM->RotateZ(Ksiphi);
artemis [22] Km_M0_S1CM->SetTwoBodyDecay(m_pip, m_pim);
artemis [23] Km_M0_S1CM->Decay();崩壊後は娘粒子の情報を取得します。
ここで注意しなくてはいけないのはDecay()で計算したときに返す重心系の情報は複合核の速度と同じように動く慣性系(S2CM系とする)のことです。
つまり、もともと考えていた
$K^{-}$の重心系(S1CM系)ではないということです。
今回の場合はS1CM系での複合核の運動はS2Lab系での運動と等価です。
よってGetDaughterをつかって値を取得します。
artemis [24] TArtParticle *Km_pip1_S1CM = Km_M0_S1CM->GetDaughter(0);
artemis [25] TArtParticle *Km_pim2_S1CM = Km_M0_S1CM->GetDaughter(1);このようにして、三つの粒子の重心系での4元ベクトルを計算できたので、あとは実験室系に変換するだけです。 Boostするベクトルは $K^{-}$の運動です。
artemis [26] TArtParticle *Km_pim1_S1Lab = new TArtParticle( Km_pim1_S1CM->Vect(), Km_pim1_S1CM->E() );
artemis [27] TArtParticle *Km_pim2_S1Lab = new TArtParticle( Km_pim2_S1CM->Vect(), Km_pim2_S1CM->E() );
artemis [28] TArtParticle *Km_pip1_S1Lab = new TArtParticle( Km_pip1_S1CM->Vect(), Km_pip1_S1CM->E() );
artemis [29] Km_pim1_S1Lab->Boost( VecSLab );
artemis [30] Km_pim2_S1Lab->Boost( VecSLab );
artemis [31] Km_pip1_S1Lab->Boost( VecSLab );このようにして計算ができました。 あとで結果のチェックを行いますが、その前にDalitz PlotおよびSquare Dalitz Plotを計算方法を書いておきます。
artemis [32] TLorentzVector LVec_M12_S1CM = static_cast<TLorentzVector>(*Km_pim1_S1CM) + static_cast<TLorentzVector>(*Km_pip1_S1CM);
artemis [33] TLorentzVector LVec_M23_S1CM = static_cast<TLorentzVector>(*Km_pip1_S1CM) + static_cast<TLorentzVector>(*Km_pim2_S1CM);
artemis [34] TArtParticle *Km_M12_S1CM = new TArtParticle( LVec_M12_S1CM.Vect(), LVec_M12_S1CM.E() );
artemis [35] TArtParticle *Km_M23_S1CM = new TArtParticle( LVec_M23_S1CM.Vect(), LVec_M23_S1CM.E() );
artemis [36] TVector3 Vec12 = Km_pim1_S1CM->Vect() + Km_pip1_S1CM->Vect();
artemis [37] Double_t DalitzM2_12 = Km_M12_S1CM->M();
artemis [38] Double_t DalitzM2_23 = Km_M23_S1CM->M();
artemis [39] Double_t DalitzMPrim = TMath::ACos( 2. * (Km_M12_S1CM->M() - M12_Min)/(M12_Max - M12_Min) - 1.0) / TMath::Pi();
artemis [40] Double_t DalitzTheta = Vec12.Theta() / TMath::Pi();とはいえこちらも乱数で放出角度を決めているため定まった値にはなりません。 あとでモンテカルロシミュレーションを行なってこのPlotが正しい範囲内にいる確認しましょう。
最後に重心系と実験室系と運動量ベクトルの和がただしいことを確認しましょう。 まずは重心系です。
artemis [41] Km_pim1_S1CM->Px()+Km_pip1_S1CM->Px()+Km_pim2_S1CM->Px()
(double) 0.0000000
artemis [42] Km_pim1_S1CM->Py()+Km_pip1_S1CM->Py()+Km_pim2_S1CM->Py()
(double) -7.1054274e-15
artemis [43] Km_pim1_S1CM->Pz()+Km_pip1_S1CM->Pz()+Km_pim2_S1CM->Pz()
(double) -1.4210855e-14良さそうですね。桁落ちで0になっていないのはしょうがないですね。 次に実験室系です。
artemis [44] Km_pim1_S1Lab->Px()+Km_pip1_S1Lab->Px()+Km_pim2_S1Lab->Px()
(double) 0.0000000
artemis [45] Km_pim1_S1Lab->Py()+Km_pip1_S1Lab->Py()+Km_pim2_S1Lab->Py()
(double) -7.1054274e-15
artemis [46] Km_pim1_S1Lab->Pz()+Km_pip1_S1Lab->Pz()+Km_pim2_S1Lab->Pz()
(double) 1000.0000こちらも良さそうです。 ちなみにDalitz Plotの値は以下の通りです。
artemis [47] DalitzM2_12
(double) 297.59458
artemis [48] DalitzM2_23
(double) 354.08724
artemis [49] DalitzMPrim
(double) 0.66949477
artemis [50] DalitzTheta
(double) 0.15027964