ハドロン二体反応のモンテカルロシミュレーションPart1
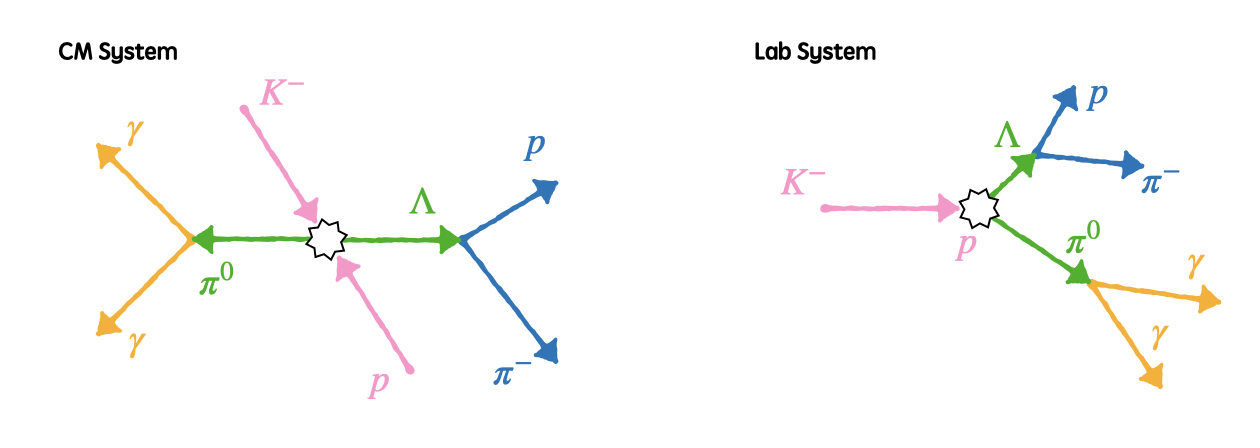
$K^{-} + p \rightarrow \pi^{0} + \Lambda$反応を計算する。(2体反応)の紹介した二体反応計算を行なってシミュレーションを行うマクロを作成します。 ここではより実際の実験に近い状況にしたいので、生成粒子も崩壊するという状況も考慮します。 このケースは図示すると以下のようになります。
マクロ中身をざっくり説明すると以下のような感じです。
- Loopの中にで反応計算を行う。
TTreeに詰める。output/sim.hadron.2body.rootに保存する。
以下にマクロを示します。
void CalcHadron2BodyReactionTempl(Int_t imax=100000){
TDatabasePDG* gPDGMassTable = new TDatabasePDG();
// Create Tree and root
TFile *file = new TFile("./output/sim.hadron.2body.root", "RECREATE");
TTree *tree = new TTree("tree", "Data Tree");
TArtParticle *fKmBeam = NULL ;
TArtParticle *fLambdaCM = NULL ;
TArtParticle *fPi0CM = NULL ;
TArtParticle *fGamma1CM = NULL ;
TArtParticle *fGamma2CM = NULL ;
TArtParticle *fProCM = NULL ;
TArtParticle *fPimCM = NULL ;
TArtParticle *fLambdaLab = NULL ;
TArtParticle *fPi0Lab = NULL ;
TArtParticle *fGamma1Lab = NULL ;
TArtParticle *fGamma2Lab = NULL ;
TArtParticle *fProLab = NULL ;
TArtParticle *fPimLab = NULL ;
tree->Branch("BeamLab" , &fKmBeam );
tree->Branch("LambdaCM" , &fLambdaCM );
tree->Branch("Pi0CM" , &fPi0CM );
tree->Branch("Gamma1CM" , &fGamma1CM );
tree->Branch("Gamma2CM" , &fGamma2CM );
tree->Branch("ProtonCM" , &fProCM );
tree->Branch("PiMinusCM" , &fPimCM );
tree->Branch("LambdaLab" , &fLambdaLab);
tree->Branch("Pi0Lab" , &fPi0Lab );
tree->Branch("Gamma1Lab" , &fGamma1Lab);
tree->Branch("Gamma2Lab" , &fGamma2Lab);
tree->Branch("ProtonLab" , &fProLab );
tree->Branch("PiMinusLab", &fPimLab );
//Generate Beam Particle
TArtParticle *KmBeam = new TArtParticle();
KmBeam->SetXYZM(0,0,1000.,gPDGMassTable->GetParticle("K-")->Mass()*1000.);
for(Int_t i=0;i<imax;i++){
///////////////////////////////////////////
// //
// K- + p -> Λ + π0 -> γ + γ + p + π- //
// //
///////////////////////////////////////////
// Generate Pre Reaction Particle K- + p with( K- + p ->[ M ]-> Lambda + pi0) reaction
TArtParticle *KmPr_Km_S1CM = KmBeam;
TArtParticle *KmPr_Pr1_S1CM = new TArtParticle();
KmPr_Pr1_S1CM->SetKineticEnergy(0, gAtomicMassTable->GetNucleusMass(1,1));
// Calculate Scattered Particle
TLorentzVector KmPr_M0_LVec_S1CM = static_cast<TLorentzVector>(*KmPr_Km_S1CM) + static_cast<TLorentzVector>(*KmPr_Pr1_S1CM);
TArtParticle *KmPr_M0_S1CM = new TArtParticle(KmPr_M0_LVec_S1CM.Vect(), KmPr_M0_LVec_S1CM.E() );
KmPr_M0_S1CM->SetTwoBodyDecay(gPDGMassTable->GetParticle("Lambda0")->Mass()*1000.,gPDGMassTable->GetParticle("pi0")->Mass()*1000.);
KmPr_M0_S1CM->Decay();
//Get Scattered Particle
TArtParticle *KmPr_Lm_S1CM = KmPr_M0_S1CM->GetDaughterAtRest(0);
TArtParticle *KmPr_Pi0_S1CM = KmPr_M0_S1CM->GetDaughterAtRest(1);
TArtParticle *KmPr_Lm_S1Lab = KmPr_M0_S1CM->GetDaughter(0);
TArtParticle *KmPr_Pi0_S1Lab = KmPr_M0_S1CM->GetDaughter(1);
//Calculate pi0 Decay
TArtParticle *KmPr_M1_S2CM = new TArtParticle( KmPr_Pi0_S1CM->Vect(), KmPr_Pi0_S1CM->E() );
KmPr_M1_S2CM->SetTwoBodyDecay(0.,0.);
KmPr_M1_S2CM->Decay();
TArtParticle *KmPr_Gamma1_S2CM = KmPr_M1_S2CM->GetDaughterAtRest(0);
TArtParticle *KmPr_Gamma2_S2CM = KmPr_M1_S2CM->GetDaughterAtRest(1);
TArtParticle *KmPr_Gamma1_S1CM = KmPr_M1_S2CM->GetDaughter(0);
TArtParticle *KmPr_Gamma2_S1CM = KmPr_M1_S2CM->GetDaughter(1);
TArtParticle *KmPr_Gamma1_S1Lab = new TArtParticle( KmPr_Gamma1_S1CM->Vect(), KmPr_Gamma1_S1CM->E() );
TArtParticle *KmPr_Gamma2_S1Lab = new TArtParticle( KmPr_Gamma2_S1CM->Vect(), KmPr_Gamma2_S1CM->E() );
KmPr_Gamma1_S1Lab->Boost( KmPr_M0_S1CM->BoostVector() );
KmPr_Gamma2_S1Lab->Boost( KmPr_M0_S1CM->BoostVector() );
//Calculate Lamda Decay
TArtParticle *KmPr_M2_S3CM = new TArtParticle( KmPr_Lm_S1CM->Vect(), KmPr_Lm_S1CM->E() );
KmPr_M2_S3CM->SetTwoBodyDecay( gAtomicMassTable->GetNucleusMass(1,1), gPDGMassTable->GetParticle("pi-")->Mass()*1000. );
KmPr_M2_S3CM->Decay();
TArtParticle *KmPr_Pr2_S3CM = KmPr_M2_S3CM->GetDaughterAtRest(0);
TArtParticle *KmPr_Pim_S3CM = KmPr_M2_S3CM->GetDaughterAtRest(1);
TArtParticle *KmPr_Pr2_S1CM = KmPr_M2_S3CM->GetDaughter(0);
TArtParticle *KmPr_Pim_S1CM = KmPr_M2_S3CM->GetDaughter(1);
TArtParticle *KmPr_Pr2_S1Lab = new TArtParticle( KmPr_Pr2_S1CM->Vect(), KmPr_Pr2_S1CM->E() );
TArtParticle *KmPr_Pim_S1Lab = new TArtParticle( KmPr_Pim_S1CM->Vect(), KmPr_Pim_S1CM->E() );
KmPr_Pr2_S1Lab->Boost( KmPr_M0_S1CM->BoostVector() );
KmPr_Pim_S1Lab->Boost( KmPr_M0_S1CM->BoostVector() );
fKmBeam = KmPr_Km_S1CM;
fLambdaCM = KmPr_Lm_S1CM;
fPi0CM = KmPr_Pi0_S1CM;
fGamma1CM = KmPr_Gamma1_S1CM;
fGamma2CM = KmPr_Gamma2_S1CM;
fProCM = KmPr_Pr2_S1CM;
fPimCM = KmPr_Pim_S1CM;
fLambdaLab = KmPr_Lm_S1Lab;
fPi0Lab = KmPr_Pi0_S1Lab;
fGamma1Lab = KmPr_Gamma1_S1Lab;
fGamma2Lab = KmPr_Gamma2_S1Lab;
fProLab = KmPr_Pr2_S1Lab;
fPimLab = KmPr_Pim_S1Lab;
tree->Fill();
delete KmPr_Pr1_S1CM;
delete KmPr_M0_S1CM;
delete KmPr_M1_S2CM;
delete KmPr_Gamma1_S1Lab;
delete KmPr_Gamma2_S1Lab;
delete KmPr_M2_S3CM;
delete KmPr_Pr2_S1Lab;
delete KmPr_Pim_S1Lab;
}
tree->Write();
file->Close();
delete file;
delete KmBeam;
}使い方
上記のマクロは簡易的な解析環境のmacroのディレクトリにある。
ひとまず以下で実行してみよう
a -q macro/CalcHadron2BodyReactionTempl.C正しく実行できているとoutput/sim.hadron.2body.rootができているはずなので、このrootファイルを開きましょう。
a output/sim.hadron.2body.rootTTreeの中身は以下のようになっています。
artemis [0]
Attaching file output/sim.hadron.2body.root as _file0...
(TFile *) 0x5593d0a1a810
artemis [1] br
BeamLab TArtParticle
LambdaCM TArtParticle
Pi0CM TArtParticle
Gamma1CM TArtParticle
Gamma2CM TArtParticle
ProtonCM TArtParticle
PiMinusCM TArtParticle
LambdaLab TArtParticle
Pi0Lab TArtParticle
Gamma1Lab TArtParticle
Gamma2Lab TArtParticle
ProtonLab TArtParticle
PiMinusLab TArtParticle相関をみてみる
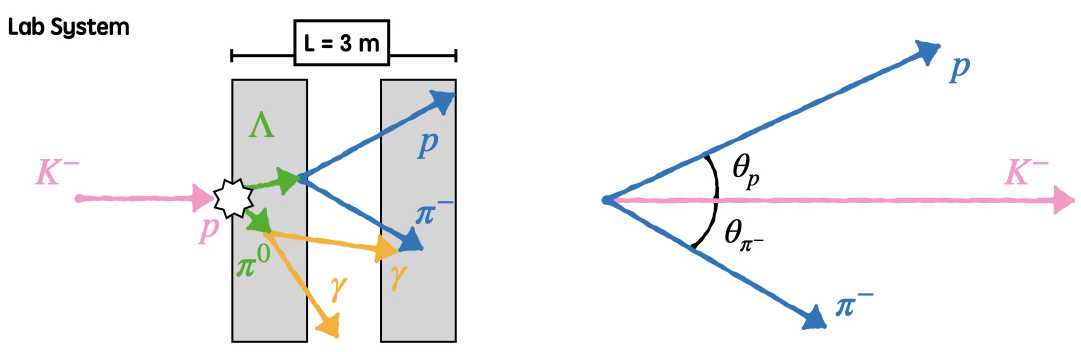
最後に相関を見てましょう。 例えば反応後に生成された粒子の崩壊から生成されたを測定する実験を行うとします。 光子はひとまず置いといて、今は陽子と $\pi^{-}$の到来時間を測定することを想定しよう。 具体的には以下のセットアップです。
左図の四角のブロックが時間を測定する検出器でそれらは3 m離れています。 それぞれの検出器で粒子を測定した時間の差(tof)を描画してみよう。 時間差の計算は以下の通りです。
$$ \Delta T_i = \frac{3}{\cos\theta_i} \frac{10^{9}}{\beta_i c} \quad [\mathrm{ns}] $$以下のようにして描画することができます。
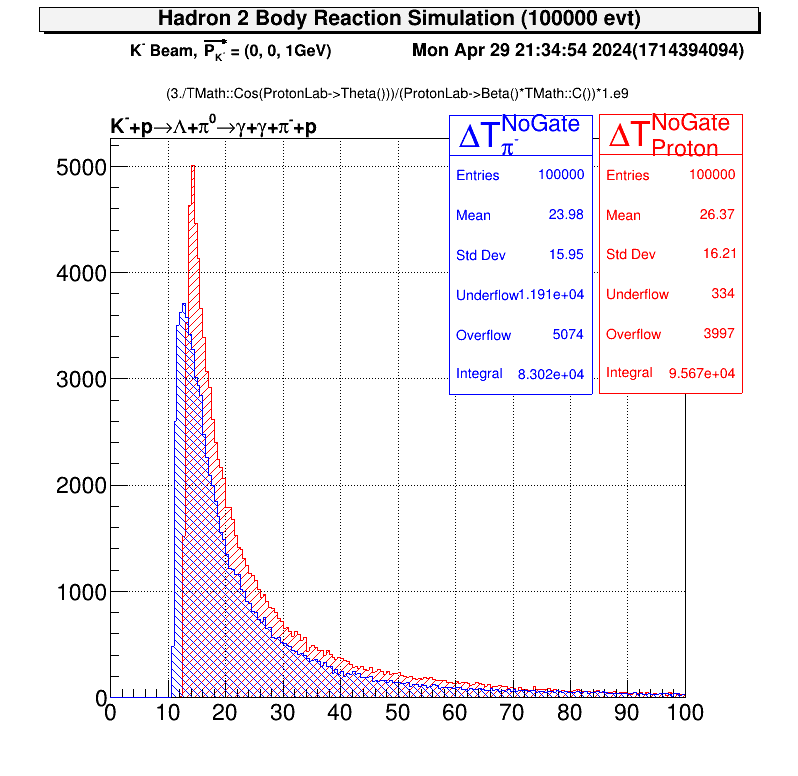
tree->Draw("(3./TMath::Cos(PiMinusLab->Theta()))/(PiMinusLab->Beta()*TMath::C())*1.e9>>#DeltaT_{#pi^{-}}^{NoGate}(200,0,100)","","colz")
tree->Draw("(3./TMath::Cos(ProtonLab->Theta()))/(ProtonLab->Beta()*TMath::C())*1.e9>>#DeltaT_{Proton}^{NoGate}(200,0,100)","","colz")次にアクセプタンスでゲートをかけてみよう。上図の光子のように角度がついていると二つ目の時間測定用の検出器を通過しないという可能性出てきます。
そのため、必ず二個目の検出器に粒子が通過するということを保証してあげましょう。
TTreeの場合Draw()メソッドの第三引数にて描画条件を指定できます。
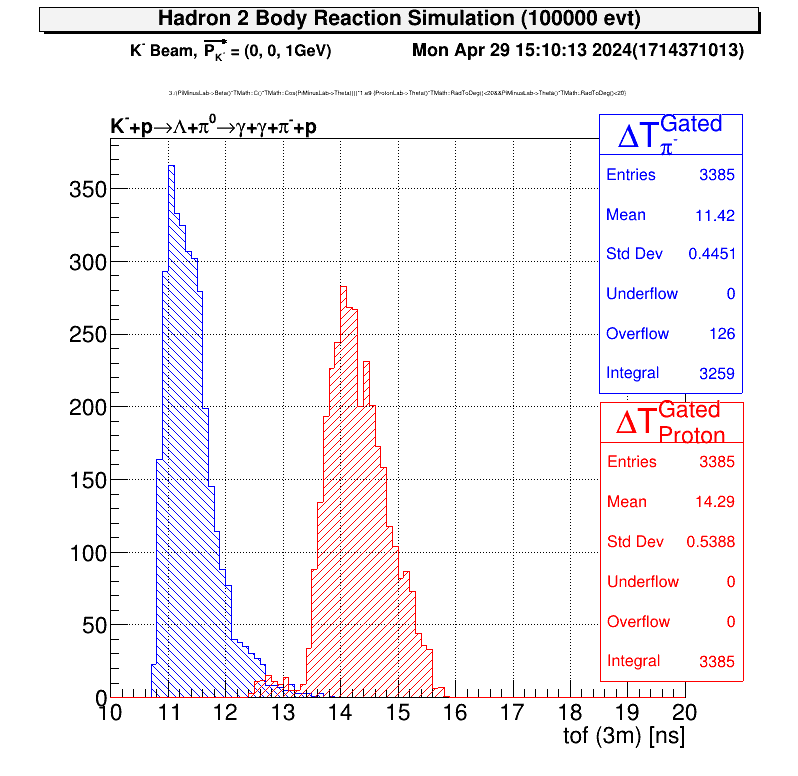
今回は角度が20度以内ということにしましょう。
その場合は以下のようにして描画できます。
tree->Draw("3./(PiMinusLab->Beta()*TMath::C()*TMath::Cos(PiMinusLab->Theta()))*1.e9>>#DeltaT_{#pi^{-}}^{Gated}(100,10,20)","ProtonLab->Theta()*TMath::RadToDeg()<20&&PiMinusLab->Theta()*TMath::RadToDeg()<20","")
tree->Draw("3./(ProtonLab->Beta()*TMath::C()*TMath::Cos(ProtonLab->Theta()))*1.e9 >>#DeltaT_{Proton}^{Gated}(100,10,20)","ProtonLab->Theta()*TMath::RadToDeg()<20&&PiMinusLab->Theta()*TMath::RadToDeg()<20","")相関は以下のようになるはずです。
| TOF Gate なし | TOF Gate あり |
|---|---|

|

|