モンテカルロ積分(N次元球体積)
Steering fileを自分で書いてみて実際にArtemisを動かしてみよう。
ここを参考に、4次元球までの体積をモンテカルロ積分で計算してみます。
Artemisで疑似乱数を生成する場合はTRandomNumberEventStoreを使えば良いです。
まずは以下のようなyamlファイルを作成します。
ここてはファイル名をhoge.yamlとしてきます。
Anchor:
- &maxevt 1000000
- &output output/sim/random_tree.root
Processor:
- name: timer
type: art::TTimerProcessor
##################################################################################################
- name: MyTRandomNumberEventStore
type: art::TRandomNumberEventStore
parameter:
Max: 1 # [Float_t] the maximum value
MaxLoop: *maxevt # [Int_t] the maximum number of loop
Min: 0 # [Float_t] the minimum value
OutputCollection: dim1 # [TString] output name of random values
OutputTransparency: 0 # [Bool_t] Output is persistent if false (default)
Verbose: 1 # [Int_t] verbose level (default 1 : non quiet)
##################################################################################################
- name: MyTRandomNumberEventStore
type: art::TRandomNumberEventStore
parameter:
Max: 1 # [Float_t] the maximum value
MaxLoop: *maxevt # [Int_t] the maximum number of loop
Min: 0 # [Float_t] the minimum value
OutputCollection: dim2 # [TString] output name of random values
OutputTransparency: 0 # [Bool_t] Output is persistent if false (default)
Verbose: 1 # [Int_t] verbose level (default 1 : non quiet)
##################################################################################################
- name: MyTRandomNumberEventStore
type: art::TRandomNumberEventStore
parameter:
Max: 1 # [Float_t] the maximum value
MaxLoop: *maxevt # [Int_t] the maximum number of loop
Min: 0 # [Float_t] the minimum value
OutputCollection: dim3 # [TString] output name of random values
OutputTransparency: 0 # [Bool_t] Output is persistent if false (default)
Verbose: 1 # [Int_t] verbose level (default 1 : non quiet)
##################################################################################################
- name: MyTRandomNumberEventStore
type: art::TRandomNumberEventStore
parameter:
Max: 1 # [Float_t] the maximum value
MaxLoop: *maxevt # [Int_t] the maximum number of loop
Min: 0 # [Float_t] the minimum value
OutputCollection: dim4 # [TString] output name of random values
OutputTransparency: 0 # [Bool_t] Output is persistent if false (default)
Verbose: 1 # [Int_t] verbose level (default 1 : non quiet)
##################################################################################################
- name: MyTOutputTreeProcessor
type: art::TOutputTreeProcessor
parameter:
FileName: *output # [TString] The name of output file
OutputTransparency: 0 # [Bool_t] Output is persistent if false (default)
SplitLevel: 0 # [Int_t] Split level of tree defined in TTree (default is changed to be 0)
TreeName: tree # [TString] The name of output tree
Verbose: 1 # [Int_t] verbose level (default 1 : non quiet)
##################################################################################################次にartemisを起動します。
VNCを使う場合はDISPLAY=:`cat $vncdisplay` artemis -l $*を、使用しない場合はartemis -lを叩けば起動できます。
artemisが起動したら、add hoge.yaml、resを順番に実行し、解析を開始します。
TTimerProessorを入れているので解析が終わると以下のメッセージが出てきます。
Info in <art::TTimerProcessor::PostLoop>: real = 5.25, cpu = 5.21 sec, total 1000000 events, rate 191938.58 evts/secfcd 0でtreeのあるディレクトリに移動します。
正しく移動できていれば、brコマンドでyamlファイルで設定した名前でブランチができているはずです。
artemis [4] fcd 0
artemis [4] br
dim1 art::TSimpleData
dim2 art::TSimpleData
dim3 art::TSimpleData
dim4 art::TSimpleData
モンテカルロ積分では領域内の被積分関数の期待を求める計算手法です。
N次元球の場合は、
$$ \mathrm{condition} = \left| \sum_{i=1}^{N} {r_i}^2 \right| < 1 $$なのでtree->Draw("branch_name","condition","")で結果を描画することができます。
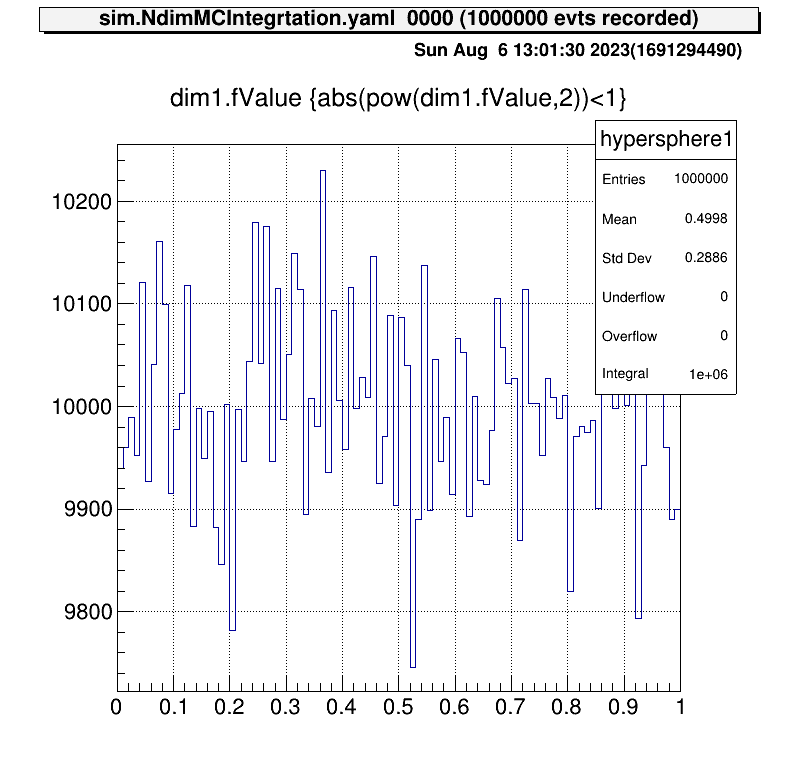
tree->Draw("dim1.fValue>>hypersphere1(100,0,1)","abs(pow(dim1.fValue,2))<1","colz")
tree->Draw("dim1.fValue:dim2.fValue>>hypersphere2(100,0,1,100,0,1)","abs(pow(dim1.fValue,2)+pow(dim2.fValue,2))<1","colz")
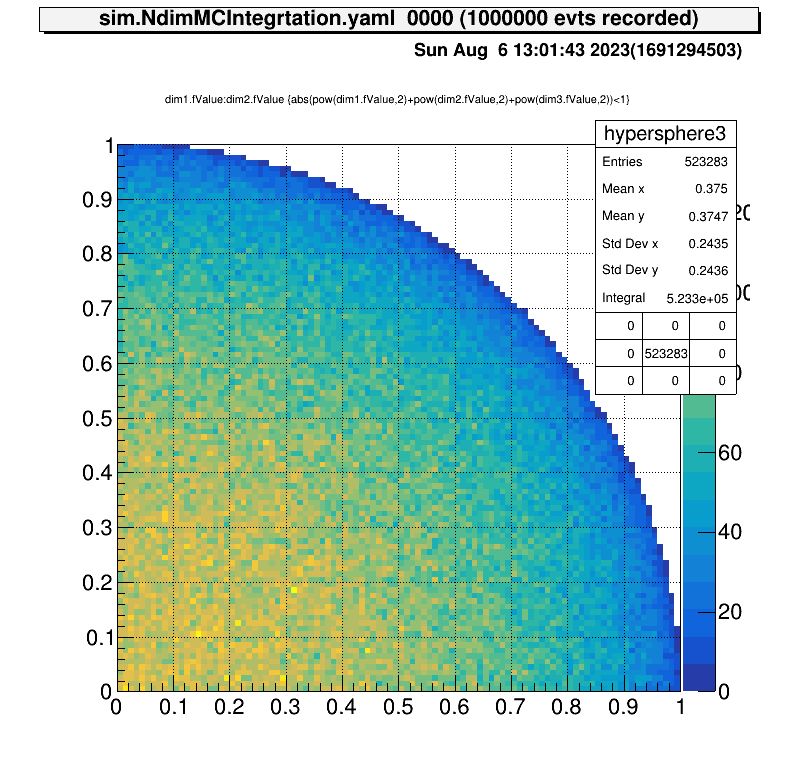
tree->Draw("dim1.fValue:dim2.fValue>>hypersphere3(100,0,1,100,0,1)","abs(pow(dim1.fValue,2)+pow(dim2.fValue,2)+pow(dim3.fValue,2))<1","colz")
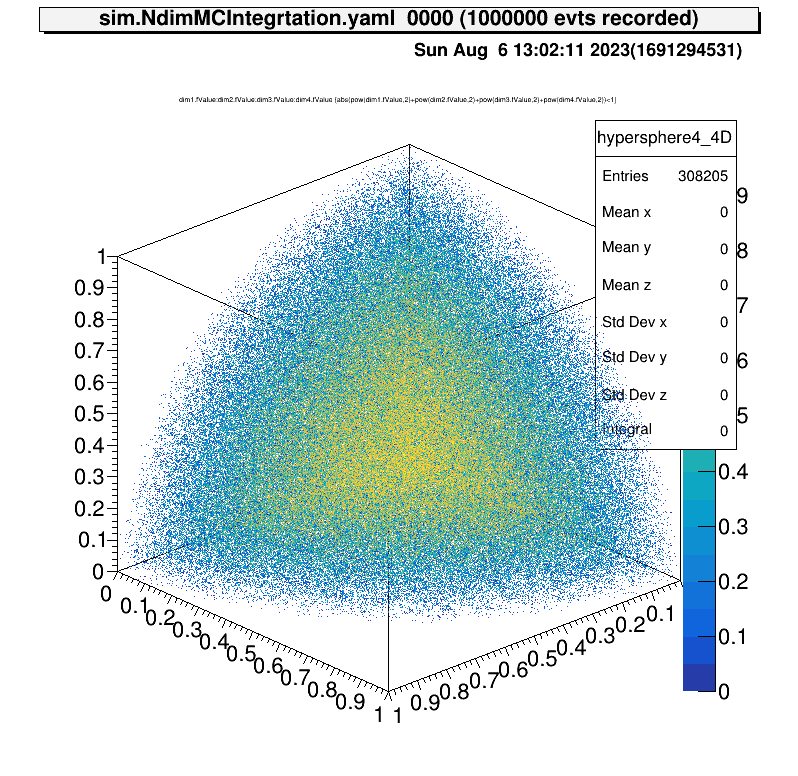
tree->Draw("dim1.fValue:dim2.fValue>>hypersphere4(100,0,1,100,0,1)","abs(pow(dim1.fValue,2)+pow(dim2.fValue,2)+pow(dim3.fValue,2)+pow(dim4.fValue,2))<1","colz")
tree->Draw("dim1.fValue:dim2.fValue:dim3.fValue:dim4.fValue>>hypersphere4_4D","abs(pow(dim1.fValue,2)+pow(dim2.fValue,2)+pow(dim3.fValue,2)+pow(dim4.fValue,2))<1","colz")| $N=1$ | $N=2$ | $N=3$ | $N=4$ |
|---|---|---|---|
 |

 |
 |
 |
本題の積分を計算していきます。
発生させた乱数の個数(loopを回した回数)と条件に入った個数の商が積分値です。
今回は区間が$[ 0,1 ]$なのでファクターとして$2^N$をかける必要があります。
analysisInfoにはloopを回した回数などの解析の情報が入っています。
今回使いたいのはloop数なのでanalysisInfo->GetAnalyzedEventNumber()を使います。
Tip
analysisInfo->ls()でメソッドの一覧が見れます。
また条件に入った個数は、先ほど作成した図のエントリー数に対応していますので、histogram_name->GetEntries()でOKです。
よって以下のコマンドで計算できます。
hypersphere1->GetEntries()/analysisInfo->GetAnalyzedEventNumber()*2.
hypersphere2->GetEntries()/analysisInfo->GetAnalyzedEventNumber()*4.
hypersphere3->GetEntries()/analysisInfo->GetAnalyzedEventNumber()*8.
hypersphere4->GetEntries()/analysisInfo->GetAnalyzedEventNumber()*16.これにて計算できました。
ちなみにちゃんと計算した時の値は以下のように計算できます。
Double_t r=1;
pow(r,1)*pow(TMath::Pi(),0)*2.
pow(r,2)*pow(TMath::Pi(),1)*1.
pow(r,3)*pow(TMath::Pi(),1)*(4./3.)
pow(r,4)*pow(TMath::Pi(),2)*(1./2.)最後に比較をしてみます。
Double_t r=1;
abs(hypersphere1->GetEntries()/analysisInfo->GetAnalyzedEventNumber()*2.-pow(r,1)*pow(TMath::Pi(),0)*2.)
abs(hypersphere2->GetEntries()/analysisInfo->GetAnalyzedEventNumber()*4.-pow(r,2)*pow(TMath::Pi(),1)*1.)
abs(hypersphere3->GetEntries()/analysisInfo->GetAnalyzedEventNumber()*8.-pow(r,3)*pow(TMath::Pi(),1)*(4./3.))
abs(hypersphere4->GetEntries()/analysisInfo->GetAnalyzedEventNumber()*16.-pow(r,4)*pow(TMath::Pi(),2)*(1./2.))返ってくる値を見ればわかりますが、3次元の時点で精度が悲しい感じになっています。
loop(yamlファイルの2行目maxevtの値)を変えて解析しなおしたり、一次元の図を眺めてみたりなどして原因を考えてみましょう。