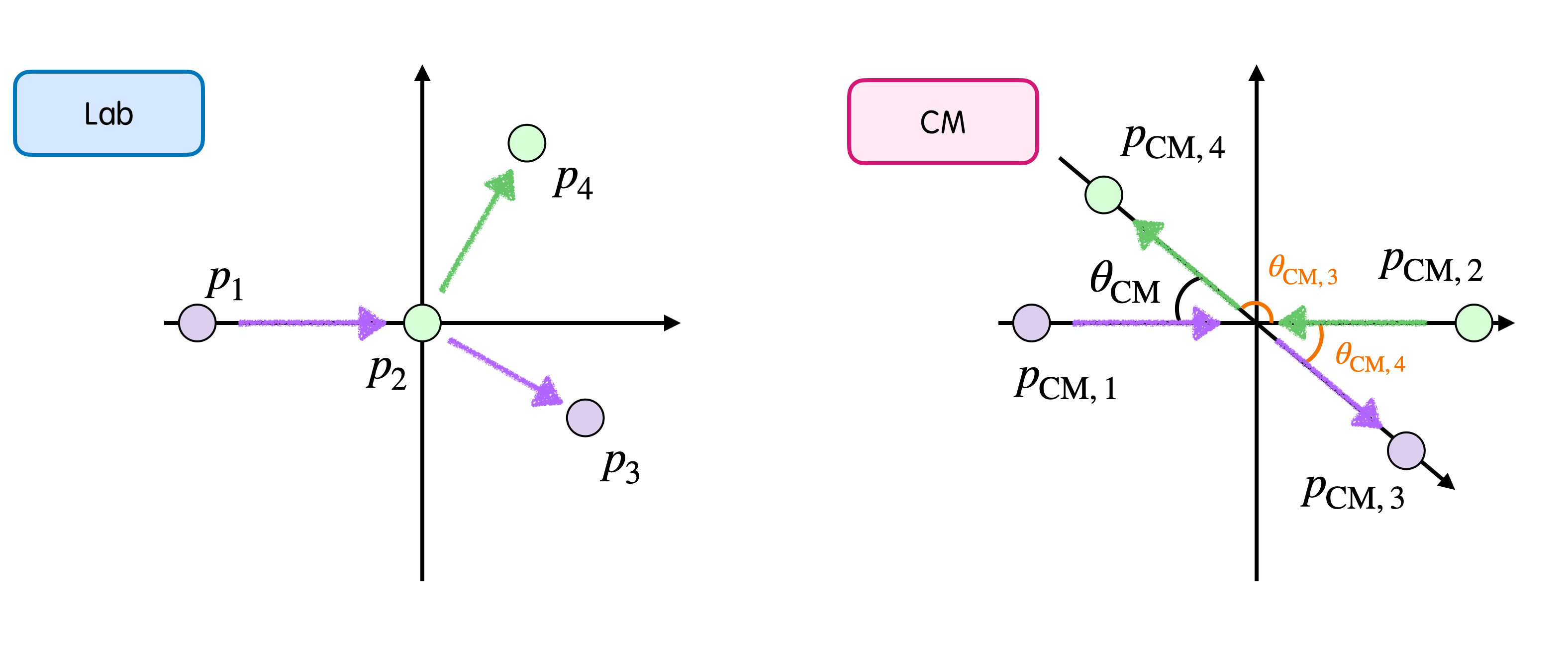
2体反応シミュレーション

Steering fileを自分で書いてみて実際にArtemisを動かしてみようPart2。

今回は2体反応のシミュレーションを行います。

以下のような条件を想定しています。

実験室系で考えると、ビーム粒子Particle1と静止している反応標的Particle2が、散乱粒子Particle3と反跳粒子Paricle4となる反応です。

以下のようなyamlファイルを作成します。

Anchor:
  - &maxevt 100000
  - &output output/sim/reaction_tree.root
Processor:
  - name: timer
    type: art::TTimerProcessor
##################################################################################################
  - name: MyTProcessor
    type: art::TBinaryReactionGenerator
    parameter:
      AngDistFile: ""  # [TString] file name of the angular distribution. The format of content is '%f %f'. 
      AngMom: 0  # [Int_t] angular momentum for bessel function. If -1 (default), the isotopic distribution is assumed.
      AngRange: [0, 15]  # [FloatVec_t] the range of angular distribution
      DoRandomizePhi: 1  # [Int_t] Flag to randomize phi direction (uniform)
      ExMean: 15  # [Float_t] mean of excitation energy
      ExRange: [0, 30]  # [FloatVec_t] the range of excitation energy
      ExWidth: 7  # [Float_t] width of excitation energy : default is delta function
      KinMean: 100  # [Float_t] mean kinetic energy per nucleon
      MCTruthCollection: mctruth  # [TString] output name of MC truth
      MaxLoop: *maxevt  # [Int_t] the maximum number of loop
      OutputCollection: recoil  # [TString] output name of particle array
      OutputTransparency: 0  # [Bool_t] Output is persistent if false (default)
      Particle1: [86, 36]  # [IntVec_t] mass and atomic number for particle1
      Particle2: [2, 1]  # [IntVec_t] mass and atomic number for particle2
      Particle3: [86, 36]  # [IntVec_t] mass and atomic number for particle3
      RunName: sim  # [TString] run name
      RunNumber: 0  # [Int_t] run number
      Verbose: 1  # [Int_t] verbose level (default 1 : non quiet)
##################################################################################################
  - name: MyTOutputTreeProcessor
    type: art::TOutputTreeProcessor
    parameter:
      FileName: *output  # [TString] The name of output file
      OutputTransparency: 0  # [Bool_t] Output is persistent if false (default)
      SplitLevel: 0  # [Int_t] Split level of tree defined in TTree (default is changed to be 0)
      TreeName: tree  # [TString] The name of output tree
      Verbose: 1  # [Int_t] verbose level (default 1 : non quiet)
##################################################################################################

Tip

art::TBinaryReactionGeneratorのパラメータのいくつか変更するだけで好きな反応計算を行うことができます。

パラメータ	説明
`AngDistFile`	自作の角度分布を使用する。パスを入力する。
`AngRange`	重心系の角度分布の範囲を指定できる。
`ExMean`	励起エネルギーの平均値を指定する。
`ExRange`	励起エネルギーの範囲を指定できる。
`ExWidth`	励起エネルギー分布（ローレンツ分布）の幅を指定する。
`KinMean`	ビーム粒子のエネルギーを指定できる。[MeV/u]
`Particle`	個々の粒子のAとZを順番に指定する。

N次元球の記事同様に解析を回します。正しく解析ができている場合、以下のブランチが作られます。

artemis [37] br
recoil               TClonesArray(TArtParticle)
mctruth              TClonesArray(TArtParticle)

recoilのブランチには反跳粒子の情報が詰まっています。一方でmctruthにはそれら以外の粒子の情報が詰まっており、それぞれ0番目がビーム粒子、1番目が標的粒子、2番目が散乱粒子です。

ではそれぞれの相関を確認してみましょう。

tree->Draw("mctruth[2].Theta()*TMath::RadToDeg()>>ThetaCM(100,0,15)","","")
tree->Draw("mctruth[2].fE-mctruth[2].TKE()-mctruth[0].M()>>Ex(100,0,30)","","")
tree->Draw("recoil.TKE():recoil.Theta()*TMath::RadToDeg()>>TKETheta(100,0,90,100,0,15)","","colz")

重心系散乱角度	励起エネルギー分布	運動学

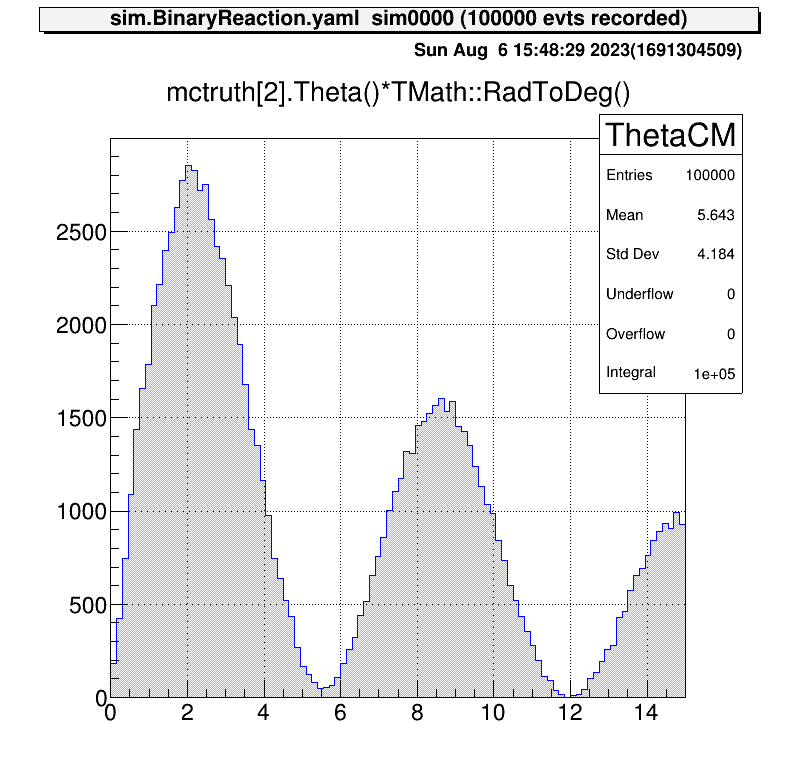
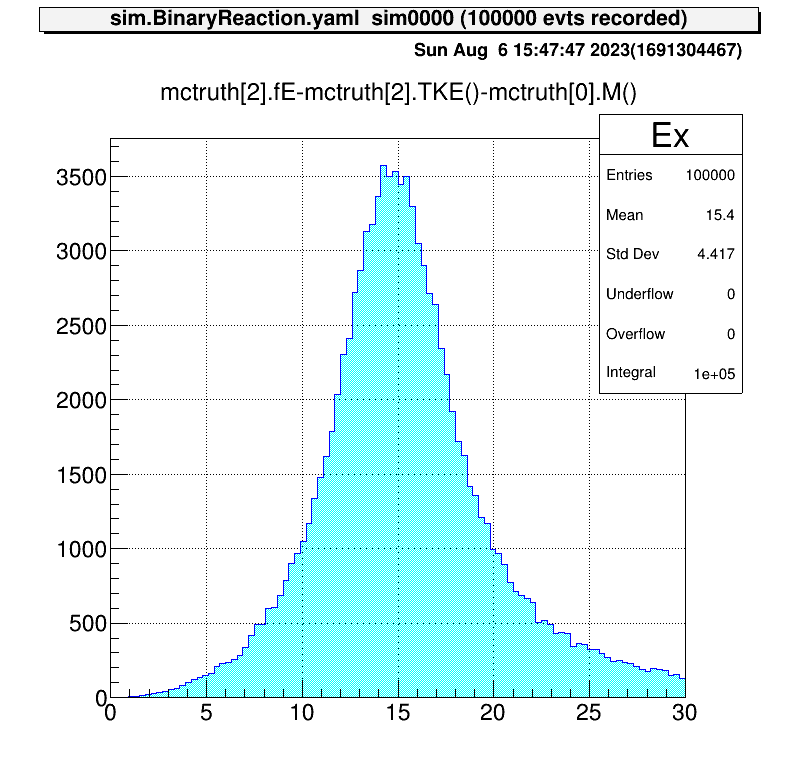
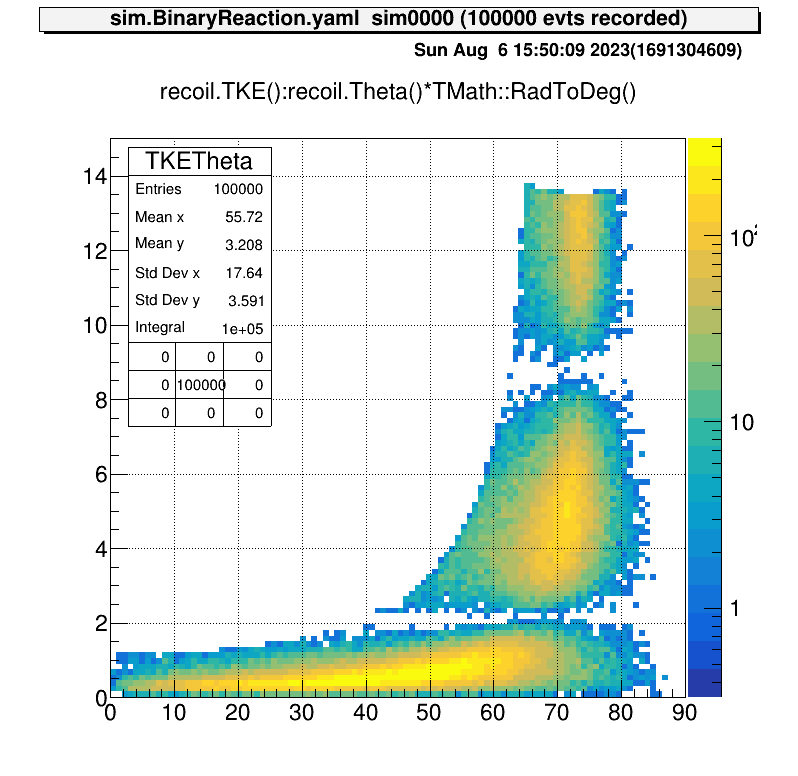
うまくできていそうですね。

Note

励起エネルギー分布は反応後エネルギーから全運動エネルギーと反応前の質量を差し引いて計算してます。