運動学曲線を描く

実験に行う上で、測定したい反応や副次的に得られる反応の反跳粒子の運動エネルギー(TKE)や反跳角度、運動量移行といった量を計算することは多いと思います。

しかし、特殊相対論での運動学の計算コードを毎回書いていくのは非常に面倒くさいですよね。（こういうところで時間を取られるのは辛いですね…）

また、実験計画を立てる上でも上記のような量およびその相関を素早く確認できると嬉しいです。

そこでここでは、反跳粒子の運動エネルギー(TKE)と反跳角度相関と運動量移行を計算するマクロを作成します。

Artemisの解析環境が正しく設定されていれば、後述するコードをコピペするだけで使えるはずです。

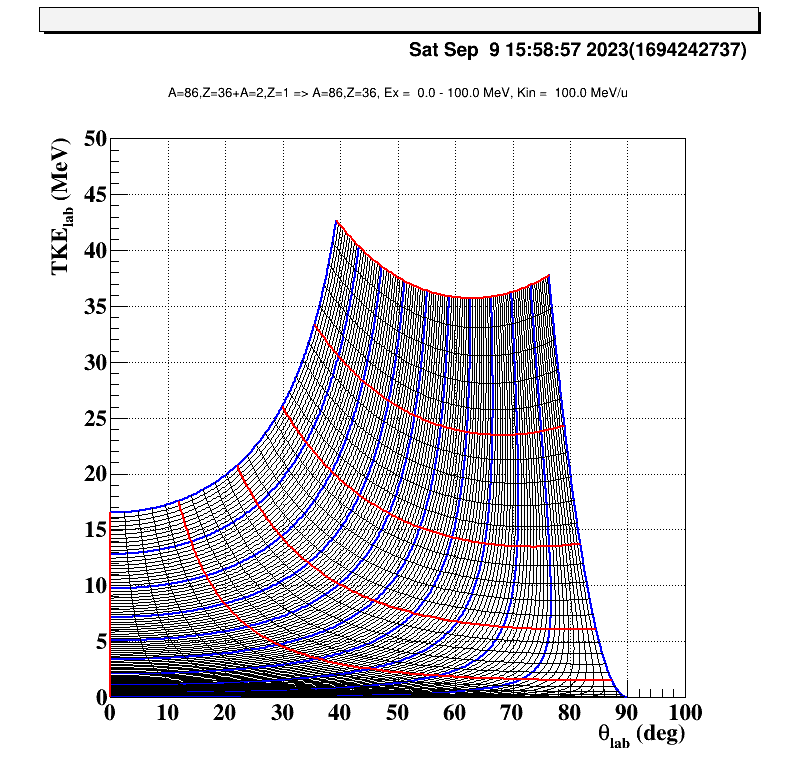
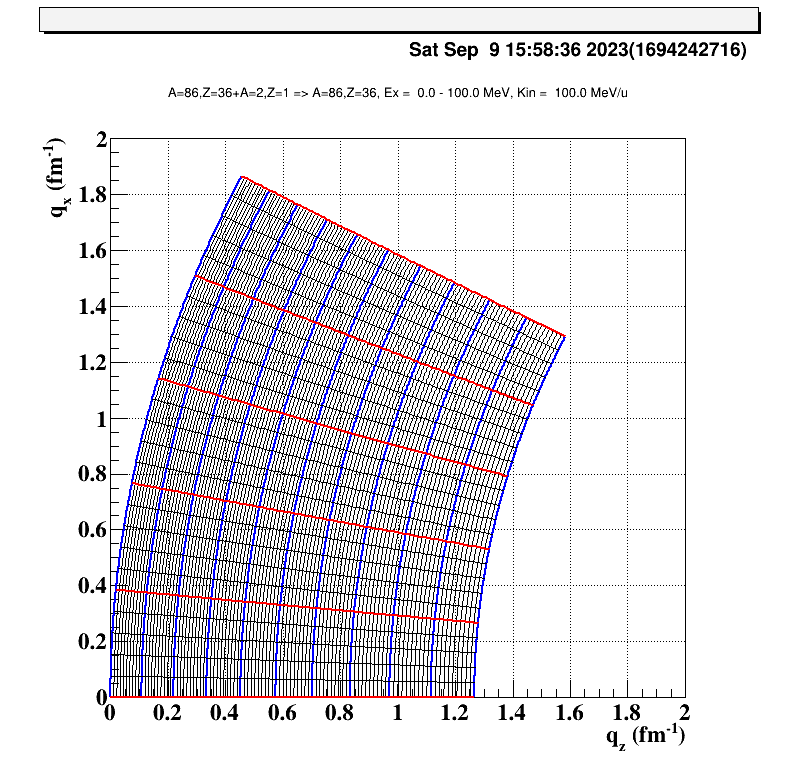
得られる図は以下のような感じになります。

反跳粒子相関	運動量移行

この図では核子あたり100 MeVまで加速した$^{86}\mathrm{Kr}$と標的の重陽子の非弾性散乱の運動学を描画しています。

縦線は86Krの励起エネルギー、横線は重心系の角度を表しています。

青線の場合は励起エネルギー(Ex)が10の倍数MeVの時の相関に、赤線の場合は重心系の角度が5の倍数度の時の相関に対応しています。

左図の場合は一番右側の青線(TKEが25 MeVの時に80度付近の点を通る線)が弾性散乱(Ex=0)における相関です。

そして、左隣の青線がExが10 MeVの線、その隣の青線が20 MeVの線…となっています。

また赤線は一番下の線が重心系の角度が0度になっており、上に行くごとに5度ずつ上がっていきます。

なので、例えば5 MeVの反跳粒子が実験室系で75度に散乱される場合、Ex=10 MeVの86Krができたことになります。

一方で右図について一番左の青線が弾性散乱に対応しています。（原点を通っているのでそれはそうでしょうと思うかもしれませんが一応書いておきます）

マクロの使い方

何はともあれ、後述するソースコードをコピーしてマクロを作成します。

作成するマクロの名前はソースコードのメインの関数と同じにしておくと良いです。ここではkinema.Cとmomentumtransfer.Cとしておくと良いです。

作成したらArtemisを起動し、以下のコマンドを実行します。（運動学相関の場合は1行目を、運動量移行を計算する場合は2行目のコマンドを実行します。）

.x  macro/kinema.C(86,36,2,1,86,36,100,0,100,1,25)
.x  macro/momentumtransfer.C(86,36,2,1,86,36,100,0,100,1,25)

ヒント

引数については以下の通りです。

引数	パラメータ	説明
1	`Int_t a1`	入射粒子の質量数
2	`Int_t z1`	入射粒子の陽子数
3	`Int_t a2`	標的粒子の質量数
4	`Int_t z2`	標的粒子の陽子数
5	`Int_t a3`	散乱粒子の質量数
6	`Int_t z3`	散乱粒子の陽子数
7	`Double_t energyPerNucleon`	入射粒子の入射エネルギー (MeV/u)
8	`Double_t exmin`	計算する励起エネルギーの最小値
9	`Double_t exmax`	計算する励起エネルギーの最大値
10	`Double_t estep`	計算する励起エネルギーの刻み幅
11	`Double_t degmax`	計算する重心系の角度の最大値

マクロの中身

後述するソースコードを見ると、一見複雑なのですが、TGraphなどを使ったことがある人がよくよくみるとほとんどが描画するためのコードだとわかると思います。

重要なのは以下の5箇所です。

TCatTwoBodyKinematics *aelkin = new TCatTwoBodyKinematics(a1, z1, a2, z2, a3, z3);
ferelkin->SetIncidentEnergy(energyPerNucleon);
relkin->SetExcitationEnergy(ex);
relkin->SetTheta(theta * TMath::DegToRad() );
const TArtParticle *recoil = relkin->GetParticle(3);

TCatTwoBodyKinematicsが一番肝の部分です。

このクラスは反応前後の粒子の種類や入射エネルギー、励起エネルギー、角度を設定してやることで反応後の粒子（または崩壊粒子）の4元ベクトルを計算してくれます。

SetIncidentEnergy()やSetExcitationEnergy()、SetTheta()はそれぞれ入射エネルギーや励起エネルギー、角度を設定する関数です。

そして、GetParticle()がTCatTwoBodyKinematics内の粒子の情報を格納しているクラスTArtParticleを読み出します。

kinema.C (運動学相関)

// Calculate Kinematics (TKE vs Theta Lab)
// Reaction ( 1 + 2 -> 3 + 4)
//     Injection Particle : 1
//     Target Particle : 2
//     Scatterd Partcle : 3
//     Recoil Particle :4
// Input Parameter Description  
//     a1 : Mass Number for Injection Particle
//     z1 : Proton Number for Injection Particle
//     a2 : Mass Number for Target Particle
//     z2 : Proton Number for Target Particle
//     a3 : Mass Number for Scatterd Partcle
//     z3 : Proton Number for Scatterd Partcle
//     energyPerNucleon : Beam Energy (MeV/u)
//     exmin : Minimum Excitation Energy
//     exmax : Maximum Excitation Energy
//     estep : Calcultion Step for Excitation Energy
//     degmax : Maximum Angle in CM System
//
void kinema(Int_t a1, Int_t z1, Int_t a2, Int_t z2, Int_t a3, Int_t z3, 
            Double_t energyPerNucleon, Double_t exmin, Double_t exmax, Double_t estep, Double_t degmax) {
  
  gROOT->ProcessLine("zone");
  TCatTwoBodyKinematics *relkin = new TCatTwoBodyKinematics(a1, z1, a2, z2, a3, z3);
  
  relkin->SetIncidentEnergy(energyPerNucleon);
  
 
 Int_t nEx = (exmax - exmin) / estep + 1;
  Int_t nQ = degmax*10+1;
  
  Double_t QStep = 0.1;
  Int_t nQLine = (nQ - 1) * QStep + 1;
  
  TGraph **grEx = new TGraph *[nEx];
  TGraph **grTh = new TGraph *[nQLine];
  
  for (Int_t iq = 0; iq != nQLine; iq++) {
    grTh[iq] = new TGraph(nEx);
  }
  
  for (Int_t iEx = 0; iEx != nEx; iEx++) {
    Double_t ex = iEx * estep + exmin;
    ex = (ex > exmax) ? exmax : ex; 
    relkin->SetExcitationEnergy(ex);
    const TArtParticle *recoil = relkin->GetParticle(3);
    grEx[iEx] = new TGraph(nQ);
    
    for (Int_t iq = 0; iq != nQ; iq++) {
      Double_t theta = iq * QStep;
      relkin->SetTheta(theta * TMath::DegToRad() );
      grEx[iEx]->SetPoint(iq, recoil->Theta() / TMath::DegToRad(), recoil->TKE());
    
      if (theta == int(theta)) {
        grTh[int(theta)]->SetPoint(iEx, recoil->Theta() / TMath::DegToRad(), recoil->TKE());
      }   
    }   
  }

  if (gDirectory->Get("h")) {
    delete gDirectory->Get("h");
  }
  
  TH2F *h2 = new TH2F("h", "", 180, 0., 180., 100, 0., 100.);
  h2->SetXTitle("#theta_{lab} (deg)");
  h2->SetYTitle("TKE_{lab} (MeV)");
  h2->GetXaxis()->SetLabelFont(22);
  h2->GetXaxis()->SetTitleFont(22);
  h2->GetYaxis()->SetLabelFont(22);
  h2->GetYaxis()->SetTitleFont(22);

  h2->SetTitle(TString::Format("A=%d,Z=%d+A=%d,Z=%d => A=%d,Z=%d, Ex = %4.1f - %4.1f MeV, Kin = %6.1f MeV/u",
                               a1, z1, a2, z2, a3, z3, exmin, exmax, energyPerNucleon));
  
  h2->SetStats(kFALSE);
  h2->Draw();
  
  for (Int_t iEx = 0; iEx < nEx; iEx++) {
    Double_t ex = iEx * estep + exmin;
    ex = (ex > exmax) ? exmax : ex; 
    
    if (int(ex / 10.) == int(ex) / 10.) {
      printf("%d %f\n", int(ex / 10.), int(ex) / 10.);
      grEx[iEx]->SetLineColor(kBlue);
      grEx[iEx]->SetLineWidth(2);
    }   
    
    grEx[iEx]->Draw("C");
 
 }

  for (Int_t iq = 0; iq < nQLine; iq++) {
    if ((iq % 5) == 0) {
      grTh[iq]->SetLineColor(kRed);
      grTh[iq]->SetLineWidth(2);
    }   
   
   grTh[iq]->Draw("C");
  
  }

}

momentumtransfer.C (運動量移行)

// Calculate Kinematics (Momentum Space)
// Reaction ( 1 + 2 -> 3 + 4)
//     Injection Particle : 1
//     Target Particle : 2
//     Scatterd Partcle : 3
//     Recoil Particle :4
// Input Parameter Description  
//     a1 : Mass Number for Injection Particle
//     z1 : Proton Number for Injection Particle
//     a2 : Mass Number for Target Particle
//     z2 : Proton Number for Target Particle
//     a3 : Mass Number for Scatterd Partcle
//     z3 : Proton Number for Scatterd Partcle
//     energyPerNucleon : Beam Energy (MeV/u)
//     exmin : Minimum Excitation Energy
//     exmax : Maximum Excitation Energy
//     estep : Calcultion Step for Excitation Energy
//     degmax : Maximum Angle in CM System
//
void momentumtransfer( Int_t a1, Int_t z1, Int_t a2, Int_t z2, Int_t a3, Int_t z3, 
                       Double_t energyPerNucleon, Double_t exmin, Double_t exmax, Double_t estep, Double_t degmax ){
  
  gROOT->ProcessLine("zone");
  TCatTwoBodyKinematics *relkin =  new TCatTwoBodyKinematics(a1, z1, a2, z2, a3, z3); 

  relkin->SetIncidentEnergy(energyPerNucleon);
  
  Int_t nEx = (exmax - exmin) / estep + 1;
  Int_t nQ = degmax*10+1;
  
  Double_t QStep = 0.1;
  Int_t nQLine = (nQ - 1) * QStep + 1;
  
  TGraph **grEx = new TGraph *[nEx];
  TGraph **grTh = new TGraph *[nQLine];
  
  for (Int_t iq = 0; iq != nQLine; iq++) {
    grTh[iq] = new TGraph(nEx);
  }
  
  for (Int_t iEx = 0; iEx != nEx; iEx++) {
    Double_t ex = iEx * estep + exmin;
    ex = (ex > exmax) ? exmax : ex; 
    relkin->SetExcitationEnergy(ex);
    const TArtParticle *recoil = relkin->GetParticle(3);
    grEx[iEx] = new TGraph(nQ);
    
    for (Int_t iq = 0; iq != nQ; iq++) {
      Double_t theta = iq * QStep;
      relkin->SetTheta(theta * TMath::DegToRad() );
      grEx[iEx]->SetPoint(iq, abs(recoil->Pz()/197.) , abs(recoil->Px()/197.));
    
      if (theta == int(theta)) {
        grTh[int(theta)]->SetPoint(iEx, abs(recoil->Pz()/197.), abs(recoil->Px()/197.));
      }   
    }   
  }
  
  if (gDirectory->Get("h")) {
    delete gDirectory->Get("h");
  }
  
  TH2F *h2 = new TH2F("h", "", 100, 0, 2.0, 100, 0, 2.0);
  h2->SetXTitle("q_{z} (fm^{-1})");
  h2->SetYTitle("q_{x} (fm^{-1})");
  h2->GetXaxis()->SetLabelFont(22);
  h2->GetXaxis()->SetTitleFont(22);
  h2->GetYaxis()->SetLabelFont(22);
  h2->GetYaxis()->SetTitleFont(22);

  h2->SetTitle(TString::Format("A=%d,Z=%d+A=%d,Z=%d => A=%d,Z=%d, Ex = %4.1f - %4.1f MeV, Kin = %6.1f MeV/u",
                               a1, z1, a2, z2, a3, z3, exmin, exmax, energyPerNucleon) );

  h2->SetStats(kFALSE);
  h2->Draw();
  
  for (Int_t iEx = 0; iEx < nEx; iEx++) {
    Double_t ex = iEx * estep + exmin;
    ex = (ex > exmax) ? exmax : ex; 
    
    if (int(ex / 10.) == int(ex) / 10.) {
      printf("%d %f\n", int(ex / 10.), int(ex) / 10.);
      grEx[iEx]->SetLineColor(kBlue);
      grEx[iEx]->SetLineWidth(2);
    }   
    
    grEx[iEx]->Draw("C");
  
  }

  for (Int_t iq = 0; iq < nQLine; iq++) {
    if ((iq % 5) == 0) {
      grTh[iq]->SetLineColor(kRed);
      grTh[iq]->SetLineWidth(2);
    }   
   
   grTh[iq]->Draw("C");
  
  }

}