2体反応(ハドロン)
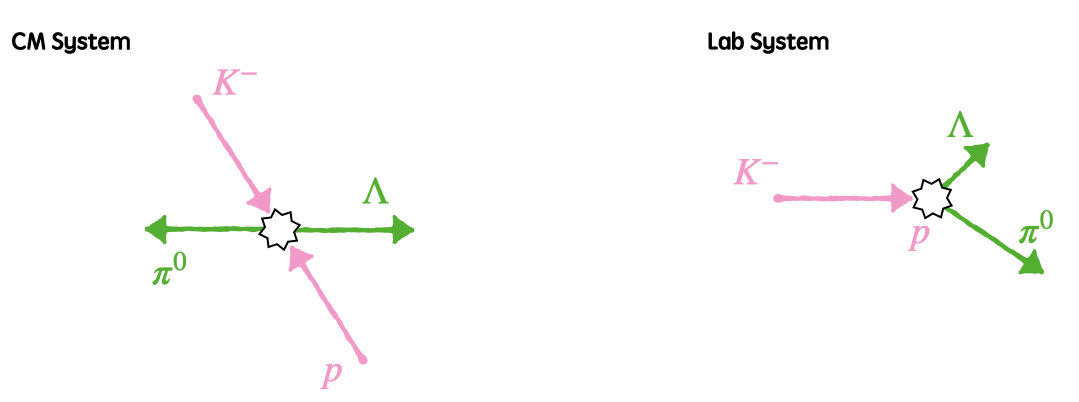
$\pi^{-}$の寿命・飛行距離計算で使用したクラスを使用してもう少し高度な計算を行なってみたいと思います。 ここでは $K^{-} + p \rightarrow \pi^{0} + \Lambda$反応を計算してみたいと思います。 反応前の状況としては固定標的pに対して運動量で1 GeVまで加速した $K^{-}$が入射される感じです。 図示すると以下のとおりです。
最後に計算してみるが、今回生成される粒子の寿命は短く実験においては $\pi^{0}$や $\Lambda$の娘粒子を測定することになりますが、ここでは気にしません。 この後のモンテカルロをするマクロでは気にして見ようと思います。モンテカルロについてはここを参照してください。
念の為グローバル変数を再定義します。
artemis [0] TDatabasePDG* gPDGMassTable = new TDatabasePDG();まず反応前の粒子である $K^{-}$および $p$を生成します。
artemis [0] TArtParticle *KmLab = new TArtParticle();
artemis [1] KmLab->SetXYZM(0,0,1000,gPDGMassTable->GetParticle("K-")->Mass()*1000.);
artemis [2] TArtParticle *ProtonLab = new TArtParticle();
artemis [3] ProtonLab->SetXYZM(0,0,0, gAtomicMassTable->GetNucleusMass(1,1));上記のコマンドでそれぞれの粒子を生成しました。
ここでは計算の簡単化のため加速方向はビーム軸(Z軸)にしました。
また、陽子の質量についてはArtemisのグローバル変数gAtomicMassTableを使用します。
この変数はTArtAtomicMassTableというクラスが元になっています。。
Artemisのソースコードを見るとどのようなメソッドがあるか確認できます。
リンクは
TArtAtomicMassTable.h
と
TArtAtomicMassTable.cc
です。
次に崩壊前の状態生成します。
崩壊前の状態は反応前の粒子の4元ベクトルの和なので以下のように計算し、新たにその複合核?状態をTArtParticleに詰めます。
artemis [4] TLorentzVector LVec_MLab = static_cast<TLorentzVector>(*KmLab) + static_cast<TLorentzVector>(*ProtonLab);
artemis [5] TArtParticle *M_KmProton = new TArtParticle( LVec_MLab.Vect(), LVec_MLab.E() );TArtParticleには二体崩壊を計算するメソッドがあるので、それを使って反応後の粒子の4元ベクトルを計算します。
まずはSetTwoBodyDecay(Double_t m1, Double_t m2, Bool_t isRandom = kTRUE)で反応後に生成される粒子の質量を定義します。
第一および第二引数で反応後に生成される質量を設定します。
一方で第三引数は反応計算する際に放出角度を乱数で生成するかどうかを設定する変数です。
このようにして反応条件を設定したのちに、Decay(Double_t theta = 0., Double_t phi = 0.)にて崩壊を計算します。
今回はランダムに生成しようと思います。
よって以下の通りです。
artemis [6] M_KmProton->SetTwoBodyDecay(gPDGMassTable->GetParticle("Lambda0")->Mass()*1000.,gPDGMassTable->GetParticle("pi0")->Mass()*1000.);
artemis [7] M_KmProton->Decay();2体反応の計算では反応前の2粒子の重心系を取るため、4元ベクトルの和を取った時空間成分の0になります。 すなわち複合核?状態の運動量は0です。 この状況は静止系の粒子の崩壊と同じ条件のため、反応計算において二体反応と粒子崩壊は同様にして計算することができます。
Decay()を行ったあとは生成粒子の情報を取得するだけです。
重心系はGetDaughterAtRest(const Int_t &i)で、実験室系はGetDaughter(const Int_t &i)で取得できます。
artemis [8] TArtParticle *Lambda0Lab = M_KmProton->GetDaughter(0);
artemis [9] TArtParticle *Lambda0CM = M_KmProton->GetDaughterAtRest(0);
artemis [10] TArtParticle *pi0Lab = M_KmProton->GetDaughter(1);
artemis [11] TArtParticle *pi0CM = M_KmProton->GetDaughterAtRest(1);最後に計算結果を見てみましょう。 まず重心系では、生成粒子の運動量ベクトルの各成分の和は0なのでそれを確認します。
artemis [12] Lambda0CM->Px() + pi0CM->Px()
(double) 0.0000000
artemis [13] Lambda0CM->Py() + pi0CM->Py()
(double) 0.0000000
artemis [14] Lambda0CM->Pz() + pi0CM->Pz()
(double) 0.0000000大丈夫そうですね。 ちなみにこの時の速度は以下の通りです。
artemis [15] Lambda0CM->Beta()
(double) 0.43447103
artemis [16] pi0CM->Beta()
(double) 0.96995921次に実験室系を見てみましょう。 一番最初の状況を思い出してみると陽子は停止しており、ビームはビーム軸(Z方向)に1 GeVで加速されています。 すなわちX軸、Y軸は0 MeV、Z軸は1000 MeVになるはずです。
artemis [17] Lambda0Lab->Px() + pi0Lab->Px()
(double) 0.0000000
artemis [18] Lambda0Lab->Py() + pi0Lab->Py()
(double) 0.0000000
artemis [19] Lambda0Lab->Pz() + pi0Lab->Pz()
(double) 1000.0000こちらもOKそうです。 この時の速度は下記の通りです。 この値はBoost方向によって変わるので同じ値になるとは限りません。
artemis [20] Lambda0Lab->Beta()
(double) 0.76048483
artemis [21] pi0Lab->Beta()
(double) 0.91542426最後に生成粒子の寿命についてみてみましょう。
artemis [22] gPDGMassTable->GetParticle("pi0")->Lifetime()
(double) 8.4278091e-17
artemis [23] gPDGMassTable->GetParticle("Lambda0")->Lifetime()
(double) 2.6317948e-10上記のように重心系においてそれぞれnsより桁で小さい寿命になっています。 この時点で相当な速度で加速しないと、実験にて直接測定するのは厳しそうなのがわかると思います。 くわえて $\pi^{0}$は中性粒子なので、そもそも測定がかなり厳しい状況にあります。 一応実験室系でみてみましょう。
artemis [24] gPDGMassTable->GetParticle("pi0")->Lifetime()*pi0Lab->Beta()*TMath::C()
(double) 2.3129051e-08
artemis [25] gPDGMassTable->GetParticle("Lambda0")->Lifetime()*Lambda0Lab->Beta()*TMath::C()
(double) 0.060001664実験室系だと $\pi^{0}$は23 nsくらいで、 $\Lambda$は60 ms程度です。 $\pi^{0}$はかなり厳しいですが、 $\Lambda$はワンチャン測定できそうなきがしなくもないです。 よって飛行距離を計算してみましょう。
artemis [26] pi0Lab->Gamma()*gPDGMassTable->GetParticle("pi0")->Lifetime()*pi0Lab->Beta()*TMath::C()
(double) 5.7464867e-08
artemis [27] Lambda0Lab->Gamma()*gPDGMassTable->GetParticle("Lambda0")->Lifetime()*Lambda0Lab->Beta()*TMath::C()
(double) 0.092401844$\pi^{0}$は話にならないですが、 $\Lambda$については9 cmのようです。 アクティブ標的とかなら測定できるのでしょうか? SNが悪くて見えなかったりするのでしょうか。 専門外なのでよくわからないですね。