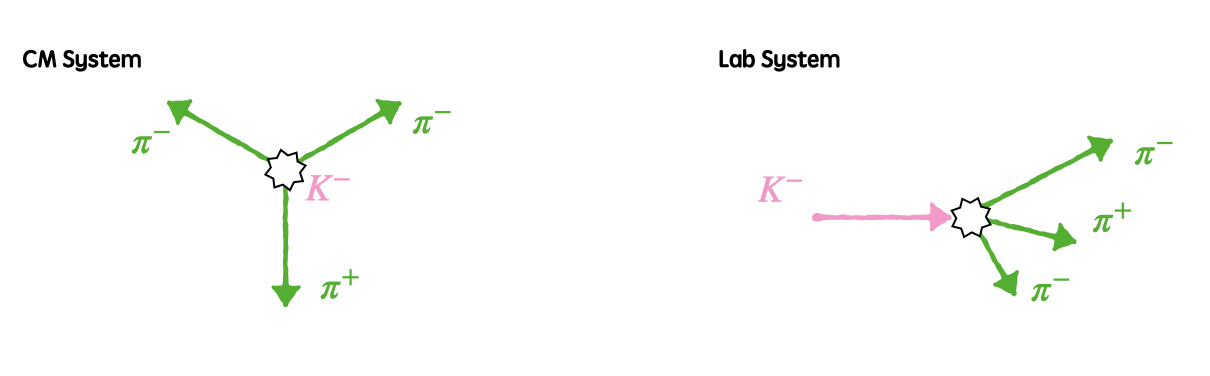ハドロン三体崩壊のモンテカルロシミュレーションPart1
$K^{-} \rightarrow \pi^{-} + \pi^{-} + \pi^{+}$反応を計算する。(3体崩壊)にて計算した三体崩壊のモンテカルロシミュレーションを行なってみましょう。 状況は以下の通りです。
マクロの概要以下のような感じです。
- Loopの中にで反応計算を行う。
TTreeに詰める。output/sim.hadron.3body.rootに保存する
ソースコードは以下の通りです。
void CalcHadron3BodyReactionTempl(Int_t imax=100000){
TDatabasePDG* gPDGMassTable = new TDatabasePDG();
// Create Tree and root
TFile *file = new TFile("./output/sim.hadron.3body.root", "RECREATE");
TTree *tree = new TTree("tree", "Data Tree");
TArtParticle *fKmBeam = NULL ;
TArtParticle *fPim1CM = NULL ;
TArtParticle *fPim2CM = NULL ;
TArtParticle *fPip1CM = NULL ;
TArtParticle *fPim1Lab = NULL ;
TArtParticle *fPim2Lab = NULL ;
TArtParticle *fPip1Lab = NULL ;
Double_t DalitzM2_12 ;
Double_t DalitzM2_23 ;
Double_t DalitzMPrim ;
Double_t DalitzTheta ;
tree->Branch("BeamLab" , &fKmBeam );
tree->Branch("PiMinus1CM" , &fPim1CM );
tree->Branch("PiMinus2CM" , &fPim2CM );
tree->Branch("PiPlus1CM" , &fPip1CM );
tree->Branch("PiMinus1Lab", &fPim1Lab );
tree->Branch("PiMinus2Lab", &fPim2Lab );
tree->Branch("PiPlus1Lab" , &fPip1Lab );
tree->Branch("DalitzM2_12",&DalitzM2_12);
tree->Branch("DalitzM2_23",&DalitzM2_23);
tree->Branch("DalitzMPrime",&DalitzMPrim);
tree->Branch("DalitzThetaPrime",&DalitzTheta);
//Set Mass
const Double_t m_Km = gPDGMassTable->GetParticle("K-")->Mass()*1000.;
const Double_t m_pim = gPDGMassTable->GetParticle("pi-")->Mass()*1000.;
const Double_t m_pip = gPDGMassTable->GetParticle("pi+")->Mass()*1000.;
//Generate Beam Particle
TArtParticle *KmBeam = new TArtParticle();
KmBeam->SetXYZM(0,0,1000.,gPDGMassTable->GetParticle("K-")->Mass()*1000.);
for(Int_t i=0;i<imax;i++){
///////////////////////////
// //
// K- -> π- + π- + π+ //
// Particle 1 : π- //
// Particle 2 : π+ //
// Particle 3 : π- //
// //
///////////////////////////
TArtParticle *Km_S1CM = KmBeam;
const TVector3 VecSLab = Km_S1CM->BoostVector();
const Double_t M12_Min = m_pim + m_pip;
const Double_t M12_Max = m_Km - m_pim;
const Double_t M23_S1CM = gRandom->Uniform(M12_Min, M12_Max);
const Double_t P23_S1CM_Nume1 = TMath::Power(m_Km, 2) - TMath::Power(M23_S1CM+m_pim, 2);
const Double_t P23_S1CM_Nume2 = TMath::Power(m_Km, 2) - TMath::Power(M23_S1CM-m_pim, 2);
const Double_t P23_S1CM = TMath::Sqrt(P23_S1CM_Nume1*P23_S1CM_Nume2)/(2.*m_Km);
TArtParticle *Km_pim1_S1CM = new TArtParticle();
TArtParticle *Km_M0_S1CM = new TArtParticle();
Km_pim1_S1CM->SetPxPyPzE( 0., 0., P23_S1CM, TMath::Sqrt(m_pim*m_pim+P23_S1CM*P23_S1CM) );
Km_M0_S1CM->SetXYZM( 0., 0., -P23_S1CM, M23_S1CM );
const Double_t Ksitheta = TMath::ACos(2 * gRandom->Uniform() - 1.);
const Double_t Ksiphi = gRandom->Uniform(0.,2.*TMath::Pi());
Km_pim1_S1CM->RotateY(Ksitheta);
Km_pim1_S1CM->RotateZ(Ksiphi);
Km_M0_S1CM->RotateY(Ksitheta);
Km_M0_S1CM->RotateZ(Ksiphi);
Km_M0_S1CM->SetTwoBodyDecay(m_pip, m_pim);
Km_M0_S1CM->Decay();
TArtParticle *Km_pip1_S1CM = Km_M0_S1CM->GetDaughter(0);
TArtParticle *Km_pim2_S1CM = Km_M0_S1CM->GetDaughter(1);
TArtParticle *Km_pim1_S1Lab = new TArtParticle( Km_pim1_S1CM->Vect(), Km_pim1_S1CM->E() );
TArtParticle *Km_pim2_S1Lab = new TArtParticle( Km_pim2_S1CM->Vect(), Km_pim2_S1CM->E() );
TArtParticle *Km_pip1_S1Lab = new TArtParticle( Km_pip1_S1CM->Vect(), Km_pip1_S1CM->E() );
Km_pim1_S1Lab->Boost( VecSLab );
Km_pim2_S1Lab->Boost( VecSLab );
Km_pip1_S1Lab->Boost( VecSLab );
fKmBeam = Km_S1CM;
fPim1CM = Km_pim1_S1CM;
fPim2CM = Km_pim2_S1CM;
fPip1CM = Km_pip1_S1CM;
fPim1Lab = Km_pim1_S1Lab;
fPim2Lab = Km_pim2_S1Lab;
fPip1Lab = Km_pip1_S1Lab;
TLorentzVector LVec_M12_S1CM = static_cast<TLorentzVector>(*Km_pim1_S1CM) + static_cast<TLorentzVector>(*Km_pip1_S1CM);
TLorentzVector LVec_M23_S1CM = static_cast<TLorentzVector>(*Km_pip1_S1CM) + static_cast<TLorentzVector>(*Km_pim2_S1CM);
TArtParticle *Km_M12_S1CM = new TArtParticle( LVec_M12_S1CM.Vect(), LVec_M12_S1CM.E() );
TArtParticle *Km_M23_S1CM = new TArtParticle( LVec_M23_S1CM.Vect(), LVec_M23_S1CM.E() );
TVector3 Vec12 = Km_pim1_S1CM->Vect() + Km_pip1_S1CM->Vect();
DalitzM2_12 = Km_M12_S1CM->M();
DalitzM2_23 = Km_M23_S1CM->M();
DalitzMPrim = TMath::ACos( 2. * (Km_M12_S1CM->M() - M12_Min)/(M12_Max - M12_Min) - 1.0) / TMath::Pi();
DalitzTheta = Vec12.Theta() / TMath::Pi();
tree->Fill();
delete Km_pim1_S1CM;
delete Km_M0_S1CM;
delete Km_pim1_S1Lab;
delete Km_pim2_S1Lab;
delete Km_pip1_S1Lab;
delete Km_M12_S1CM;
delete Km_M23_S1CM;
}
tree->Write();
file->Close();
delete file;
delete KmBeam;
}使い方
上記のマクロは簡易的な解析環境のmacroのディレクトリにあります。
ひとまず以下で実行してみよう。
a -q macro/CalcHadron3BodyReactionTempl.C正しく実行できているとoutput/sim.hadron.3body.rootができているはずなので、このrootファイルを開きましょう。
a output/sim.hadron.3body.rootTTreeの中身は以下のようになっています。
artemis [0]
Attaching file output/sim.hadron.3body.root as _file0...
(TFile *) 0x561a86a5b470
artemis [1] br
BeamLab TArtParticle
PiMinus1CM TArtParticle
PiMinus2CM TArtParticle
PiPlus1CM TArtParticle
PiMinus1Lab TArtParticle
PiMinus2Lab TArtParticle
PiPlus1Lab TArtParticle
DalitzM2_12 Double_t
DalitzM2_23 Double_t
DalitzMPrime Double_t
DalitzThetaPrime Double_t相関をみてみる。
Tree::Draw()などを使って色々描画してみましょう。
例えば以下のような図が作れるようになります。
| TOF Gate あり | 放出角度 |
|---|---|
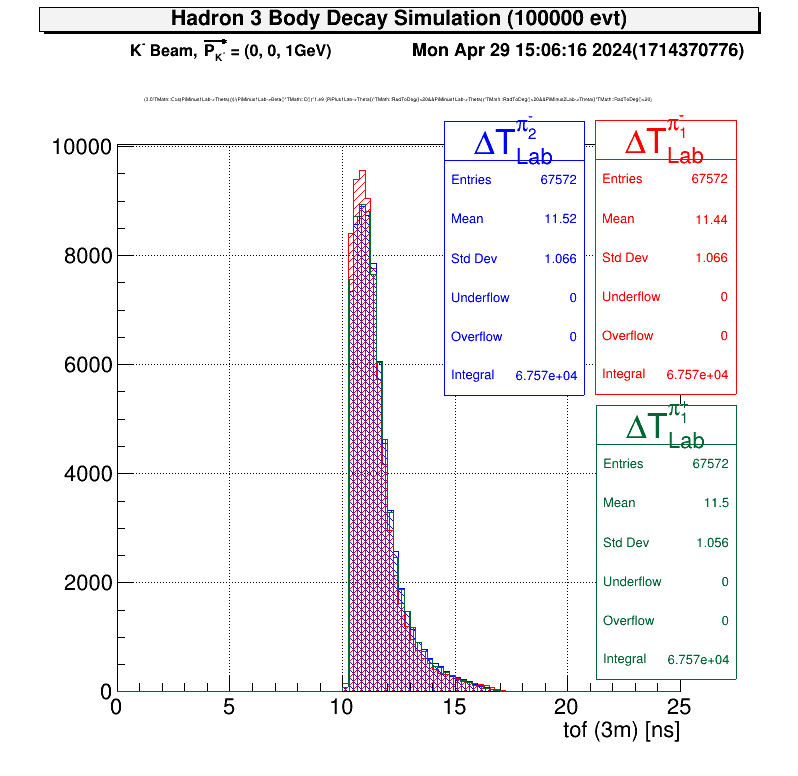

|
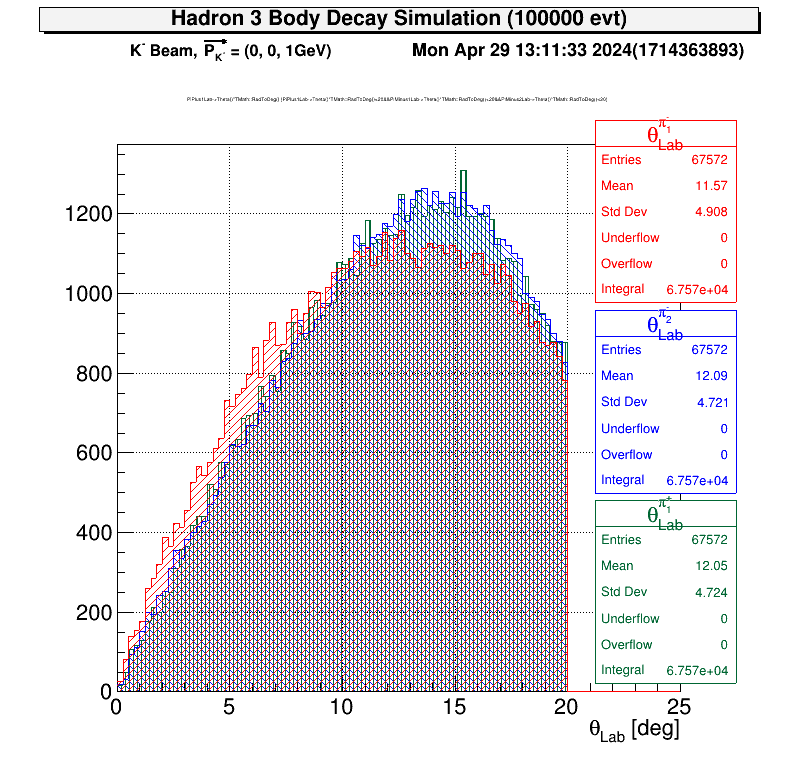

|
| Dalitz Plot | Square Dalitz Plot |
|---|---|
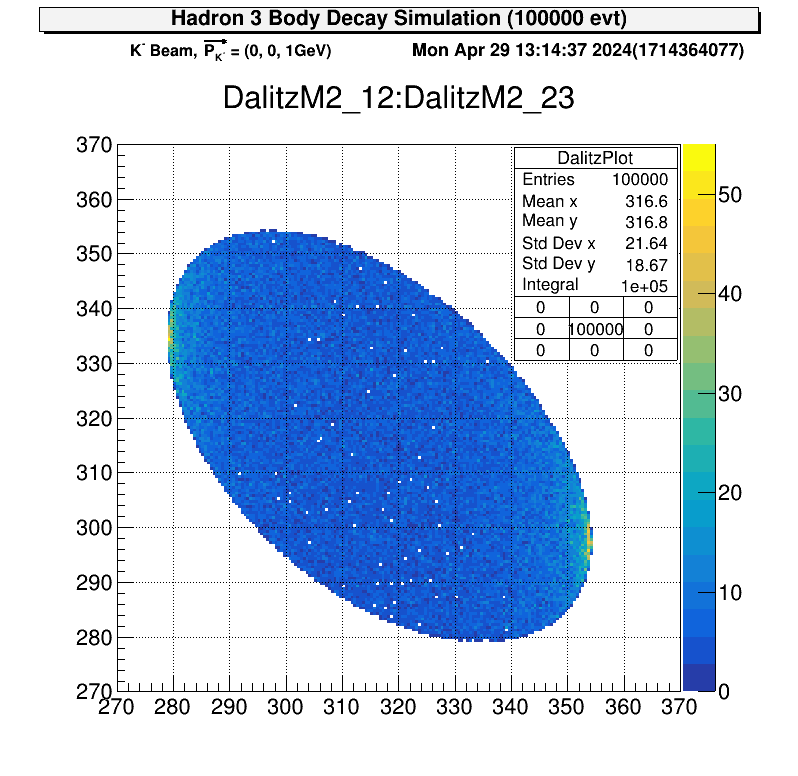

|
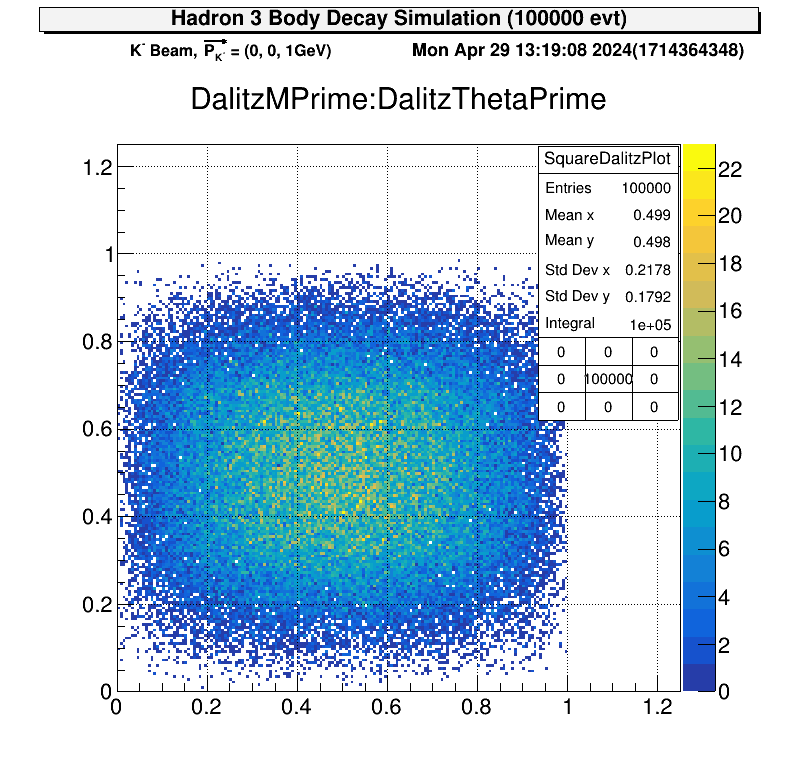

|