シェルモデル (shell model)

参考文献

以下のテキスト（講義資料）を参考に簡単なシェルモデル計算を行う。
すべてのテキストで ¹⁸O の例が出てくる(Introductory Nuclear Physics では問題 7-4 に出てくる)。¹⁶O の doubly closed shell のコアにヴァレンス中性子が 2 個のシンプルな系なので、例として良く使われるようだ。

計算

¹⁸O の基底状態の binding energy と励起状態のエネルギーを USD 相互作用を用いて計算する。この相互作用が適用されるモデルスペースは sd-shell (0d_3/2, 0d_5/2, 1s_1/2) である。USD 相互作用を記述するパラメータファイルは Nushell や oxbash に同梱されており、sps/w.int というファイルである。中身を見ると

! The "USD" interaction of B. H. Wildenthal for A=18
! For other A the two-body matrix elements should be multiplied
! by (18/A)**(0.3) and the single-particle matrix elements
! are mass independent. In OXBASH the multiplication is done 
! automatically in the subroutine SHSP.FOR
! ERROR CHANGED AUG 1988   (2   2   2   1        2   1     -0.2878000)
! ORDER:  1 = 1D3/2    2 = 1D5/2    3 = 2S1/2 
! The following spe give values of 15.63, 21.75 and 18.13 relative to 
! 40Ca (1.612 -2.684 -2.967)
   63      1.6465800     -3.9477999     -3.1635399
  1   1   1   1        0   1     -2.1845000
  1   1   1   1        1   0     -1.4151000
  1   1   1   1        2   1     -0.0665000
  1   1   1   1        3   0     -2.8842001
  2   1   1   1        1   0      0.5647000
  2   1   1   1        2   1     -0.6149000
...
...
  3   3   3   1        1   0      1.2501000
  3   3   3   3        0   1     -2.1245999

となっており、! で始まる行はコメント行であり無視する。コメント行を飛ばして考えたときの 1 行目では、 1 番目の整数が two-body matrix element (TBME) の数、2 - 4 番目の実数が 0d_3/2, 0d_5/2, 1s_1/2 軌道の single-paricle energy (SPE) (MeV 単位) を表す。SPE と 1 粒子軌道との対応は sps/sd.sp というファイルを参照している？2 行目から 64 (= 63 + 1) 行目は TBME (MeV 単位) を表す。書式は
$\begin{eqnarray*} j_1 \ \ j_2 \ \ j_3 \ \ j_4 \ \ \ \ \ \ J \ \ T\ \ \ \ \langle j_1\,j_2\,J\,T\,|V|\,j_1\,j_2\,J\,T\rangle \end{eqnarray*}$
となっており、J と T はそれぞれ spin と isospin を表す。j₁ - j₄ は 1 粒子軌道を表す整数が入り、1 : 0d_3/2, 2 : 0d_5/2, 3 : 1s_1/2, という対応となっている。整数と1 粒子軌道の対応はやはり sps/sd.sp を見ている？ sps/label.dat というファイルにも書いてある。ちなみにこの有効相互作用の SPEs (3個) と TBMEs (63 個) は元の論文 (B. H. Wildenthal, Prog. Part. Nucl. Phys. 11, 5 (1984)) や USDA, USDB の論文 (PRC74(2006)034315) にすべての要素が書いてある。このファイルより、各軌道の SPE は
$\begin{eqnarray*} \epsilon_{0d3/2} &=& 1.6465800~{\rm MeV}\\ \epsilon_{0d5/2} &=& -3.9477999~{\rm MeV}\\ \epsilon_{1s1/2} &=& -3.1635399~{\rm MeV} \end{eqnarray*}$
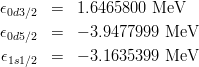
となる。
J^π = 0⁺ の場合の計算
$\begin{eqnarray*} | \Phi_1 \rangle = |0d_{3/2},0d_{3/2};J=0,T=1 \rangle\\ | \Phi_2 \rangle = |0d_{5/2},0d_{5/2};J=0,T=1 \rangle\\ | \Phi_3 \rangle = |1s_{1/2},1s_{1/2};J=0,T=1 \rangle\\ \end{eqnarray*}$
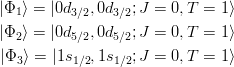
と書くとする。計算で使う TBME を抜きだせば
$\begin{eqnarray*} \langle \Phi_1|V|\Phi_1\rangle\ &=& \langle 0d_{3/2},0d_{3/2};J=0,T=1|V|0d_{3/2},0d_{3/2};J=0,T=1 \rangle = -2.1845000~{\rm MeV}\\ \langle \Phi_2|V|\Phi_1\rangle\ &=& \langle 0d_{5/2},0d_{5/2};J=0,T=1|V|0d_{3/2},0d_{3/2};J=0,T=1 \rangle = -3.1856000~{\rm MeV}\\ \langle \Phi_2|V|\Phi_2\rangle\ &=& \langle 0d_{5/2},0d_{5/2};J=0,T=1|V|0d_{5/2},0d_{5/2};J=0,T=1 \rangle = -2.8197000~{\rm MeV}\\ \langle \Phi_2|V|\Phi_3\rangle\ &=& \langle 0d_{5/2},0d_{5/2};J=0,T=1|V|1s_{1/2},1s_{1/2};J=0,T=1 \rangle = -1.3247000~{\rm MeV}\\ \langle \Phi_3|V|\Phi_1\rangle\ &=& \langle 1s_{1/2},1s_{1/2};J=0,T=1|V|0d_{3/2},0d_{3/2};J=0,T=1 \rangle = -1.0835000~{\rm MeV}\\ \langle \Phi_3|V|\Phi_3\rangle\ &=& \langle 1s_{1/2},1s_{1/2};J=0,T=1|V|1s_{1/2},1s_{1/2};J=0,T=1 \rangle = -2.1245999~{\rm MeV} \end{eqnarray*}$
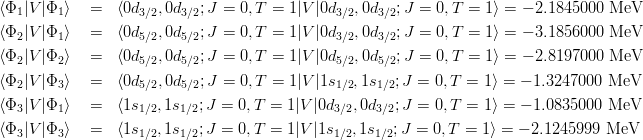
となる。これより Hamiltonian matrix elements は
$\begin{eqnarray*} H_{11} &=& 2\epsilon_{0d3/2} + \langle \Phi_1|V|\Phi_1\rangle = 2\times 1.6465800 -2.1845000 = 1.10866~{\rm MeV}\\ H_{22} &=& 2\epsilon_{0d5/2} + \langle \Phi_2|V|\Phi_2\rangle = 2\times(-3.9477999) -2.8197000 = -10.715299~{\rm MeV}\\ H_{33} &=& 2\epsilon_{1s1/2} + \langle \Phi_3|V|\Phi_3\rangle = 2\times(-3.1635399) -2.1245999 = -8.4516797~{\rm MeV}\\ H_{21} &=& H_{12} = \langle \Phi_2|V|\Phi_1\rangle = -3.1856000~{\rm MeV}\\ H_{23} &=& H_{32} = \langle \Phi_2|V|\Phi_3\rangle = -1.3247000~{\rm MeV}\\ H_{31} &=& H_{13} = \langle \Phi_3|V|\Phi_1\rangle = -1.0835000~{\rm MeV}\\ \end{eqnarray*}$
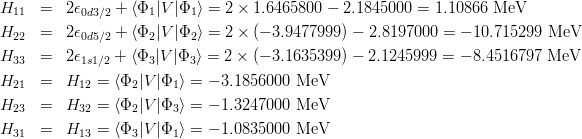
となり、Hamiltonian matrix は
$\begin{eqnarray*} \left[ \begin{array}{ccc} H_{11} & H_{12} & H_{13} \\ H_{21} & H_{22} & H_{23} \\ H_{31} & H_{32} & H_{33} \end{array} \right] = \left[ \begin{array}{ccc} 1.10866 & -3.1856000 & -1.0835000 \\ -3.1856000 & -10.715299 & -1.3247000 \\ -1.0835000 & -1.3247000 & -8.4516797 \end{array} \right] {\rm MeV} \end{eqnarray*}$
と書ける。この行列を対角化すると (ROOT での対角化はこのマクロを実行)、固有値が以下のように得られる。
$\begin{eqnarray*} \left[ \begin{array}{c} -12.171 \\ -7.85115 \\ 1.96386 \end{array} \right] {\rm MeV} \end{eqnarray*}$
これらは、以下の Nushell の計算結果と完全に一致する。

Interaction file information from go.mit       
spe taken from first line in *.int file
Interaction  spe
w             1.6466 -3.9478 -3.1635

   N  name  Njtp  T    E(MeV)   J     Ex(MeV) (* for yrast)

   1 b0202w   1   1    -12.171  0  +   0.000 *
   2 b0202w   2   1     -7.851  0  +   4.320  
   3 b0202w   3   1      1.964  0  +  14.135

J^π = 2⁺ の場合の計算
J = 2 である状態を選び、
$\begin{eqnarray*} | \Phi_1 \rangle = |0d_{3/2},0d_{3/2};J=2,T=1 \rangle\\ | \Phi_2 \rangle = |0d_{5/2},0d_{3/2};J=2,T=1 \rangle\\ | \Phi_3 \rangle = |1s_{1/2},0d_{3/2};J=2,T=1 \rangle\\ | \Phi_4 \rangle = |0d_{5/2},0d_{5/2};J=2,T=1 \rangle\\ | \Phi_5 \rangle = |1s_{1/2},0d_{5/2};J=2,T=1 \rangle\\ \end{eqnarray*}$
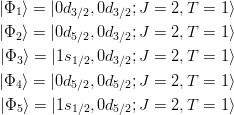
と書くとする。これより、
$\begin{eqnarray*} & & \left[ \begin{array}{ccccc} H_{11} & H_{12} & H_{13} & H_{14} & H_{15} \\ H_{21} & H_{22} & H_{23} & H_{24} & H_{25} \\ H_{31} & H_{32} & H_{33} & H_{34} & H_{35} \\ H_{41} & H_{42} & H_{43} & H_{44} & H_{45} \\ H_{51} & H_{52} & H_{53} & H_{54} & H_{55} \end{array} \right]\\ &=& \left[ \begin{array}{ccccc} 2\epsilon_{0d3/2} & 0 & 0 & 0 & 0\\ 0 & \epsilon_{0d3/2}+\epsilon_{0d5/2} & 0 & 0 & 0\\ 0 & 0 & \epsilon_{0d3/2}+\epsilon_{1s1/2} & 0 & 0\\ 0 & 0 & 0 & 2\epsilon_{0d5/2} & 0\\ 0 & 0 & 0 & 0 & \epsilon_{0d5/2}+\epsilon_{1s1/2} \end{array} \right] \\ &&+ \left[ \begin{array}{ccccc} \langle\Phi_1|V|\Phi_1\rangle & \langle\Phi_1|V|\Phi_2\rangle & \langle\Phi_1|V|\Phi_3\rangle & \langle\Phi_1|V|\Phi_4\rangle & \langle\Phi_1|V|\Phi_5\rangle\\ \langle\Phi_2|V|\Phi_1\rangle & \langle\Phi_2|V|\Phi_2\rangle & \langle\Phi_2|V|\Phi_3\rangle & \langle\Phi_2|V|\Phi_4\rangle & \langle\Phi_2|V|\Phi_5\rangle\\ \langle\Phi_3|V|\Phi_1\rangle & \langle\Phi_3|V|\Phi_2\rangle & \langle\Phi_3|V|\Phi_3\rangle & \langle\Phi_3|V|\Phi_4\rangle & \langle\Phi_3|V|\Phi_5\rangle\\ \langle\Phi_4|V|\Phi_1\rangle & \langle\Phi_4|V|\Phi_2\rangle & \langle\Phi_4|V|\Phi_3\rangle & \langle\Phi_4|V|\Phi_4\rangle & \langle\Phi_4|V|\Phi_5\rangle\\ \langle\Phi_5|V|\Phi_1\rangle & \langle\Phi_5|V|\Phi_2\rangle & \langle\Phi_5|V|\Phi_3\rangle & \langle\Phi_5|V|\Phi_4\rangle & \langle\Phi_5|V|\Phi_5\rangle \end{array} \right] \\ &=& \left[ \begin{array}{ccccc} 2\times(1.6466) & 0 & 0 & 0 & 0 \\ 0 & 1.6466-3.9478 & 0 & 0 & 0 \\ 0 & 0 & 1.64660-3.1635 & 0 & 0 \\ 0 & 0 & 0 & 2\times(-3.9478) & 0 \\ 0 & 0 & 0 & 0 & -3.9478-3.1635 \end{array} \right]\\ &&+ \left[ \begin{array}{ccccc} -0.0665 & -0.6149 & -0.5154 & -1.6221 & -0.4041 \\ -0.6149 & -0.3248 & -0.5247 & -0.2828 & -0.4770 \\ -0.5154 & -0.5247 & -0.4064 & -0.6198 & -1.9410 \\ -1.6221 & -0.2828 & -0.6198 & -1.0020 & -0.8616 \\ -0.4041 & -0.4770 & -1.9410 & -0.8616 & -0.8183 \end{array} \right]{\rm MeV}\\ &=& \left[ \begin{array}{ccccc} 3.2267 & -0.6149 & -0.5154 & -1.6221 & -0.4041 \\ -0.6149 & -2.6260 & -0.5247 & -0.2828 & -0.4770 \\ -0.5154 & -0.5247 & -1.9233 & -0.6198 & -1.9410 \\ -1.6221 & -0.2828 & -0.6198 & -8.8976 & -0.8616 \\ -0.4041 & -0.4770 & -1.9410 & -0.8616 & -7.9296 \end{array} \right]{\rm MeV} \end{eqnarray*}$
となる。この行列を対角化すると (ROOT での対角化はこのマクロを実行)、固有値が以下のように得られる。
$\begin{eqnarray*} \left[ \begin{array}{c} -9.99125 \\ -7.73236 \\ 3.52193 \\ -2.70561 \\ -1.24263 \end{array} \right] {\rm MeV} \end{eqnarray*}$
これらは、以下の Nushell の binding energy の計算結果と完全に一致する。

Interaction file information from go.mit       
spe taken from first line in *.int file
Interaction  spe
w             1.6466 -3.9478 -3.1635

   N  name  Njtp  T    E(MeV)   J     Ex(MeV) (* for yrast)

   1 b4202w   1   1     -9.991  2  +   0.000 *
   2 b4202w   2   1     -7.732  2  +   2.259  
   3 b4202w   3   1     -2.706  2  +   7.285  
   4 b4202w   4   1     -1.243  2  +   8.748  
   5 b4202w   5   1      3.522  2  +  13.513

J^π = 1⁺ の場合の計算
J = 2 の場合の計算とほぼ同じ手順となる。J = 1 である状態を選び、
$\begin{eqnarray*} | \Phi_1 \rangle = |0d_{3/2},0d_{5/2};J=1,T=1 \rangle\\ | \Phi_2 \rangle = |0d_{3/2},0s_{1/2};J=1,T=1 \rangle\\ \end{eqnarray*}$
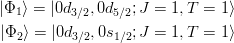
と書くとする。これより、
$\begin{eqnarray*} & & \left[ \begin{array}{ccccc} H_{11} & H_{12} \\ H_{21} & H_{22} \end{array} \right]\\ &=& \left[ \begin{array}{cc} \epsilon_{0d3/2}+\epsilon_{0d5/2} & 0\\ 0 & \epsilon_{0d3/2}+\epsilon_{1s1/2} \end{array} \right] + \left[ \begin{array}{cc} \langle\Phi_1|V|\Phi_1\rangle & \langle\Phi_1|V|\Phi_2\rangle\\ \langle\Phi_2|V|\Phi_1\rangle & \langle\Phi_2|V|\Phi_2\rangle \end{array} \right] \\ &=& \left[ \begin{array}{cc} -1.2678 & 0.1874\\ 0.1874 & -0.9104 \end{array} \right]{\rm MeV} \end{eqnarray*}$
となる。この行列を対角化すると (ROOT での対角化はこのマクロを実行)、固有値が以下のように得られる。
$\begin{eqnarray*} \left[ \begin{array}{c} -1.34806 \\ -0.830124 \end{array} \right] {\rm MeV} \end{eqnarray*}$
これらは、以下の Nushell の binding energy の計算結果と完全に一致する。

Interaction file information from go.mit       
spe taken from first line in *.int file
Interaction  spe
w             1.6466 -3.9478 -3.1635

   N  name  Njtp  T    E(MeV)   J     Ex(MeV) (* for yrast)

   1 b2202w   1   1     -1.348  1  +   0.000 *
   2 b2202w   2   1     -0.830  1  +   0.518

メモ

武藤さんの講義資料の中では上記の USD 相互作用を用いている。この有効相互作用の two-body matrix elements は B. H. Wildenthal, Prog. Part. Nucl. Phys. 11, 5 (1984) にすべての要素 (63 個) が書いてある。ちなみに元の論文では USD 相互作用という名前は出てこないようだ。また B. A. Brown and B. H. Wildenthal, Annu. Rev. Nucl. Part. Sci. 38, 29 (1988) では W 相互作用という名前が使われている。しかし USDA, USDB 相互作用の論文 (PRC74(2006)034315) では USD interaction と言っている（１個所だけ）。

シェルモデル

おぼえがき

リンク

シェルモデル (shell model)

参考文献

計算

メモ