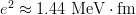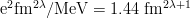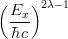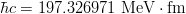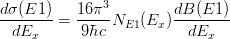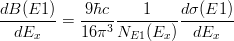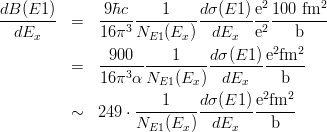Coulomb Breakup
E1, M1, E2 の仮想光子数 (nE1(ω), nM1(ω), nE2(ω))
Bertulani et al. のレポート (Physics Report 163(1988)299) の式(2.5.5a), (2.5.5b), (2.5.5c)より、E1, M1, E2 の仮想光子数 nE1(ω), nM1(ω), nE2(ω) はそれぞれ、
- となる。ここで
- π : 円周率
Z1 : 標的の陽子数
- α : 微細構造定数
c : 光の速さ
v : 入射粒子の速さ
K0, K1 : 変形ベッセル関数 (modified bessel function)
ξ=ωR/γv
- ω : 仮想光子の振動数
R : カットオフパラメータ(核同士が衝突しない最小のインパクトパラメータ)
γ : 入射粒子のローレンツ因子(
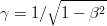 )
)
- である。実際にコンピュータで計算する場合、以下のような式変形をすると都合が良い。
ここで β=v/cであり、
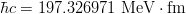 。
。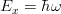 は仮想光子のエネルギーを表し、このエネルギーの光子を吸った原子核はこのエネルギー分だけ励起する。
は仮想光子のエネルギーを表し、このエネルギーの光子を吸った原子核はこのエネルギー分だけ励起する。 中村さんの論文 (PRL103(2009)262501など) のNE1(Ex) は上の nE1(ω) と同じ量であり、
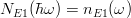 という関係である。
という関係である。
仮想光子数の計算
仮想光子数は中村さんの持っている emd ライブラリで計算できる。 emd_sub.f というファイル内で仮想光子数などの関数が定義されている。例えば、n_photon_omega という関数は E1 の仮想光子数を返す関数である。ただし、引数として ω でなく、
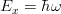 を用いているため注意が必要。また、emd_sub.f 内では変形ベッセル関数を Numerical Recipies in C の 237 ページ辺りを参考に計算しているようだ。
を用いているため注意が必要。また、emd_sub.f 内では変形ベッセル関数を Numerical Recipies in C の 237 ページ辺りを参考に計算しているようだ。
クーロン励起断面積
クーロン励起断面積σは以下のようにかける (PRC46(1992)2340)。
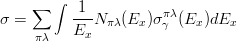 .
.
- また、励起エネルギーで微分すれば (中村さんD論より)、
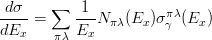 .
.
となる。ここで、πλ (=E1, M1, E2, ...) は電磁気多重極を表し、Eλ が電気2λ重極, Mλ が磁気2λ重極となる。Nπλ(Ex) は仮想光子数、
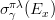 は光吸収断面積を表す。仮想光子数は無次元。光吸収断面積は面積の次元を持つ。
は光吸収断面積を表す。仮想光子数は無次元。光吸収断面積は面積の次元を持つ。 - 光吸収断面積は、以下のように書ける (PRC46(1992)2340より)。
![$$\sigma^{\pi\lambda}_\gamma(E_x) = \frac{(2\pi)^3(\lambda+1)}{\lambda[(2\lambda+1)!!]^2}\left(\frac{E_x}{\hbar c}\right)^{2\lambda-1}\frac{dB(\pi\lambda)}{dE_x}$$ $$\sigma^{\pi\lambda}_\gamma(E_x) = \frac{(2\pi)^3(\lambda+1)}{\lambda[(2\lambda+1)!!]^2}\left(\frac{E_x}{\hbar c}\right)^{2\lambda-1}\frac{dB(\pi\lambda)}{dE_x}$$](latex_dbaf4fbcda6d53f15994684f04309a4a22358783_p1.png) .
.
ここで、dB(πλ)/dEx の単位は e2fm2λ/MeV である。また、
- より、
であるから、dB(πλ)/dEx の単位は
- とも書ける。
- ここで、次元があっているかを確認すると、
- の次元は、
より、fm-(2λ-1) の次元となる。dB(πλ)/dEx は fm2λ+1 の次元を持つので、
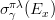 が面積の次元を持つことになる。
が面積の次元を持つことになる。
E1 強度分布の計算
クーロン励起断面積の励起エネルギーに対する分布(上記参照)で、E1 のみを考えれば、
となる。非束縛状態に励起する場合、この断面積はクーロン分解断面積の励起エネルギー分布に相当する。この式から E1 強度分布 dB(E1)/dEx を導出する場合、dB(E1)/dEx について解いた
を用いる。dσ(E1)/dEx の単位は b/MeV、dB(E1)/dEx の単位は e2fm2/MeV であるから、上の式に
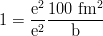 をかけて、
をかけて、 とする。ここで、100 fm2 = 1 b,
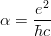 (微細構造定数(cgsガウス単位系)) を用いた。これで、ちゃんと単位が合うようになる。
(微細構造定数(cgsガウス単位系)) を用いた。これで、ちゃんと単位が合うようになる。
E1 の表記
E1 は変数ではないのでローマン体で書くのかと思いきや、中村さんは APS のエディターにイタリックでと言われたらしい。そのためか、中村さんの PRL96(2006)252502 では E1 はイタリックになっている。Bertulani さんの論文 (PRC46(1992)2340) でもイタリック。 一方で Bertulani さんの APS ではない論文 (Phys.Rep.163(1988)299, PLB650(2007)233) では、ローマン体になっている。 APS ではイタリックにすればよい?
![\begin{eqnarray}
n_{E1}(\omega) &=& \frac{2}{\pi}Z^2_1 \alpha \left(\frac{c}{v}\right)^2 \left[\xi K_0K_1-\frac{\xi^2v^2}{2c^2}(K_1^2-K_0^2)\right] \nonumber \\
n_{M1}(\omega) &=& \frac{2}{\pi}Z^2_1 \alpha \left[\xi K_0K_1-\frac{\xi^2}{2}(K_1^2-K_0^2)\right] \nonumber \\
n_{E2}(\omega) &=& \frac{2}{\pi}Z^2_1 \alpha \left(\frac{c}{v}\right)^4 \left[2\left(1-\frac{v^2}{c^2}\right) K_1^2 + \xi \left(2-\frac{v^2}{c^2}\right)^2 K_0K_1 - \frac{\xi^2v^4}{2c^4}(K_1^2-K_0^2)\right]
\nonumber
\end{eqnarray} \begin{eqnarray}
n_{E1}(\omega) &=& \frac{2}{\pi}Z^2_1 \alpha \left(\frac{c}{v}\right)^2 \left[\xi K_0K_1-\frac{\xi^2v^2}{2c^2}(K_1^2-K_0^2)\right] \nonumber \\
n_{M1}(\omega) &=& \frac{2}{\pi}Z^2_1 \alpha \left[\xi K_0K_1-\frac{\xi^2}{2}(K_1^2-K_0^2)\right] \nonumber \\
n_{E2}(\omega) &=& \frac{2}{\pi}Z^2_1 \alpha \left(\frac{c}{v}\right)^4 \left[2\left(1-\frac{v^2}{c^2}\right) K_1^2 + \xi \left(2-\frac{v^2}{c^2}\right)^2 K_0K_1 - \frac{\xi^2v^4}{2c^4}(K_1^2-K_0^2)\right]
\nonumber
\end{eqnarray}](latex_783702c7b4ed5a63065fc81ac06c9f336748d96f_p1.png)
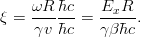
![\begin{eqnarray}
\alpha &=& \frac{e^2}{\hbar c} = \frac{1}{137.035999074} \ \ \mathrm{(in\ Gaussian\ CGS\ units)}\nonumber\\[1.5ex]
\hbar c &=& 197.326971~{\rm MeV\cdot fm} \nonumber
\end{eqnarray} \begin{eqnarray}
\alpha &=& \frac{e^2}{\hbar c} = \frac{1}{137.035999074} \ \ \mathrm{(in\ Gaussian\ CGS\ units)}\nonumber\\[1.5ex]
\hbar c &=& 197.326971~{\rm MeV\cdot fm} \nonumber
\end{eqnarray}](latex_6f6d078955cb7e2bc21f08d10766f1a9b12aafe2_p1.png)