Dipole strength distribution
Dipole strength distribution (B(E1) distribution) についてのメモ。
公式
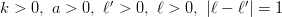 に対して、
に対して、 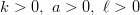 に対して、
に対して、 k > 0, a > 0 に対して、
ノート
Mathematica で積分を計算
Mathematica では k > 0, a > 0 に対する
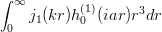 を以下の式で計算可能。
を以下の式で計算可能。 Assuming[k > 0 && a > 0, Integrate[SphericalBesselJ[1, k*r]*SphericalHankelH1[0, I*a*r]*r^3, {r, 0, Infinity}]]- うまく計算できない場合は、第一種球ハンケル関数を一度展開して計算(下記参照)。
Assuming[k > 0 && a > 0, Integrate[SphericalBesselJ[1, k*r]*FunctionExpand[SphericalHankelH1[0, I*a*r]]*r^3, {r, 0, Infinity}]]
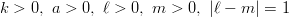 に対して
に対して 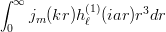 を計算するには、
を計算するには、 Assuming[k > 0 && a > 0 && m > 0 && l > 0 && Abs[l - m] == 1, Integrate[FunctionExpand[SphericalBesselJ[m, k*r]*SphericalHankelH1[l, I*a*r]*r^3], {r, 0, Infinity}]]
とする。 m を
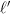 にするとなぜか計算できなかった。微分してしまっている?
にするとなぜか計算できなかった。微分してしまっている?
一般超幾何関数 (generalized hypergeometric functions) pFq
ここで、(a)k はポッホハマー記号 (Pochhammer symbol) であり、
ここで Γ(a) は ガンマ関数 であり、a > 0 に対しては、
また、p = 2, q = 1 の場合、
![\begin{eqnarray*}
{}_2F_1 (a, b ; c ; x)
&=&\sum^{\infty}_{k=0} \frac{(a)_k(b)_k}{(c)_k}\frac{x^k}{k!} \\
&=&\sum^{\infty}_{k=0} \frac{\Gamma(a+k)}{\Gamma(a)}\frac{\Gamma(b+k)}{\Gamma(b)}\frac{\Gamma(c)}{\Gamma(c+k)}\frac{x^k}{k!} \\
&=&\sum^{\infty}_{k=0} \frac{[a (a+1)\cdots(a+k-1)][(b (b+1)\cdots(b+k-1)]}{c (c+1)\cdots(c+k-1)}\frac{x^k}{k!}.
\end{eqnarray*} \begin{eqnarray*}
{}_2F_1 (a, b ; c ; x)
&=&\sum^{\infty}_{k=0} \frac{(a)_k(b)_k}{(c)_k}\frac{x^k}{k!} \\
&=&\sum^{\infty}_{k=0} \frac{\Gamma(a+k)}{\Gamma(a)}\frac{\Gamma(b+k)}{\Gamma(b)}\frac{\Gamma(c)}{\Gamma(c+k)}\frac{x^k}{k!} \\
&=&\sum^{\infty}_{k=0} \frac{[a (a+1)\cdots(a+k-1)][(b (b+1)\cdots(b+k-1)]}{c (c+1)\cdots(c+k-1)}\frac{x^k}{k!}.
\end{eqnarray*}](latex_614504cdcf52fe37a45971f17c785b6f7fc38c51_p1.png)
一般超幾何関数の特殊な場合
ガンマ関数の割り算
第一種球ハンケル関数 (参考: Spherical Hankel Function of the First Kind)
第一種球ベッセル関数 (参考: Spherical Bessel Function of the First Kind)
第二種球ベッセル関数 (参考: Spherical Bessel Function of the Second Kind)
計算(その1)
![\begin{eqnarray*}
\int_{0}^{\infty} j_{\ell'}(kr)h_\ell^{(1)}(iar)r^3dr
&=& \int_{0}^{\infty} \sqrt{\frac{\pi}{2kr}}J_{\ell'+1/2}(kr) \sqrt{\frac{\pi}{2iar}}H^{(1)}_{\ell+1/2}(iar)r^3dr \\
&=& \frac{\pi}{2\sqrt{iak}} \int_{0}^{\infty} J_{\ell'+1/2}(kr)H^{(1)}_{\ell+1/2}(iar) r^2dr \\
&=& \frac{\pi}{2\sqrt{iak}} \left[- 4(-i)^{\ell} \frac{\sqrt{iak}}{\pi} \frac{k^{\ell'} }{a^{\ell'+4}} \frac{\Gamma ((\ell' - \ell +3)/2) \Gamma ((\ell' + \ell +4)/2)}{\Gamma (\ell'+3/2)} {}_2F_1\left(\frac{\ell' - \ell +3}{2},\frac{\ell' + \ell +4}{2}; \ell'+\frac{3}{2}; -\frac{k^2}{a^2} \right)\right] \\
&=& - 2 (-i)^{\ell} \frac{k^{\ell'} }{a^{\ell'+4}} \frac{\Gamma ((\ell' - \ell +3)/2) \Gamma ((\ell' + \ell +4)/2)}{\Gamma (\ell'+3/2)} {}_2F_1\left(\frac{\ell' - \ell +3}{2},\frac{\ell' + \ell +4}{2}; \ell'+\frac{3}{2}; -\frac{k^2}{a^2} \right)
\end{eqnarray*} \begin{eqnarray*}
\int_{0}^{\infty} j_{\ell'}(kr)h_\ell^{(1)}(iar)r^3dr
&=& \int_{0}^{\infty} \sqrt{\frac{\pi}{2kr}}J_{\ell'+1/2}(kr) \sqrt{\frac{\pi}{2iar}}H^{(1)}_{\ell+1/2}(iar)r^3dr \\
&=& \frac{\pi}{2\sqrt{iak}} \int_{0}^{\infty} J_{\ell'+1/2}(kr)H^{(1)}_{\ell+1/2}(iar) r^2dr \\
&=& \frac{\pi}{2\sqrt{iak}} \left[- 4(-i)^{\ell} \frac{\sqrt{iak}}{\pi} \frac{k^{\ell'} }{a^{\ell'+4}} \frac{\Gamma ((\ell' - \ell +3)/2) \Gamma ((\ell' + \ell +4)/2)}{\Gamma (\ell'+3/2)} {}_2F_1\left(\frac{\ell' - \ell +3}{2},\frac{\ell' + \ell +4}{2}; \ell'+\frac{3}{2}; -\frac{k^2}{a^2} \right)\right] \\
&=& - 2 (-i)^{\ell} \frac{k^{\ell'} }{a^{\ell'+4}} \frac{\Gamma ((\ell' - \ell +3)/2) \Gamma ((\ell' + \ell +4)/2)}{\Gamma (\ell'+3/2)} {}_2F_1\left(\frac{\ell' - \ell +3}{2},\frac{\ell' + \ell +4}{2}; \ell'+\frac{3}{2}; -\frac{k^2}{a^2} \right)
\end{eqnarray*}](latex_33a19e33300916550587312218282569e1b64057_p1.png)
- ここで、
- を使った。
計算(その2)
具体的な表式
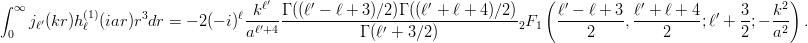
![\begin{eqnarray*}
\int_{0}^{\infty} j_{\ell+1}(kr)h_\ell^{(1)}(iar)r^3dr
&=& -2(-i)^\ell \frac{k^{\ell+1}}{a^{\ell+5}} \frac{\Gamma (2)\Gamma (\ell+5/2)}{\Gamma (\ell+5/2)} {}_2F_1\left(2,\ell+\frac{5}{2}; \ell+\frac{5}{2}; -\frac{k^2}{a^2} \right) \\
&=& -2(-i)^\ell \frac{k^{\ell+1}}{a^{\ell+1}} \frac{1}{(a^2+k^2)^2}, \\[2.0ex]
\int_{0}^{\infty} j_{\ell-1}(kr)h_\ell^{(1)}(iar)r^3dr
&=& -2(-i)^\ell \frac{k^{\ell-1}}{a^{\ell+3}} \frac{\Gamma (1)\Gamma (\ell+3/2)}{\Gamma (\ell+1/2)} {}_2F_1\left(1,\ell+\frac{3}{2}; \ell+\frac{1}{2}; -\frac{k^2}{a^2} \right) \\
&=& -(-i)^\ell \frac{k^{\ell-1}}{a^{\ell+1}} \frac{(2\ell-1)k^2+(2\ell+1)a^2}{(a^2+k^2)^2}.
\end{eqnarray*} \begin{eqnarray*}
\int_{0}^{\infty} j_{\ell+1}(kr)h_\ell^{(1)}(iar)r^3dr
&=& -2(-i)^\ell \frac{k^{\ell+1}}{a^{\ell+5}} \frac{\Gamma (2)\Gamma (\ell+5/2)}{\Gamma (\ell+5/2)} {}_2F_1\left(2,\ell+\frac{5}{2}; \ell+\frac{5}{2}; -\frac{k^2}{a^2} \right) \\
&=& -2(-i)^\ell \frac{k^{\ell+1}}{a^{\ell+1}} \frac{1}{(a^2+k^2)^2}, \\[2.0ex]
\int_{0}^{\infty} j_{\ell-1}(kr)h_\ell^{(1)}(iar)r^3dr
&=& -2(-i)^\ell \frac{k^{\ell-1}}{a^{\ell+3}} \frac{\Gamma (1)\Gamma (\ell+3/2)}{\Gamma (\ell+1/2)} {}_2F_1\left(1,\ell+\frac{3}{2}; \ell+\frac{1}{2}; -\frac{k^2}{a^2} \right) \\
&=& -(-i)^\ell \frac{k^{\ell-1}}{a^{\ell+1}} \frac{(2\ell-1)k^2+(2\ell+1)a^2}{(a^2+k^2)^2}.
\end{eqnarray*}](latex_b3cc194bc3930efd37648489ae08f2b6ca398962_p1.png)
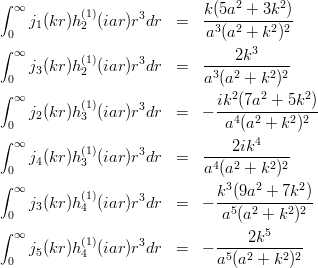
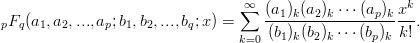
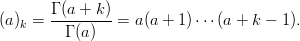
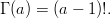
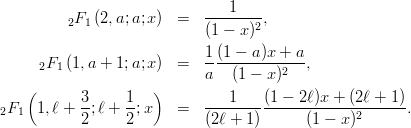
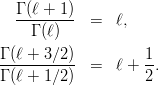
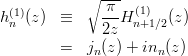
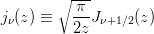
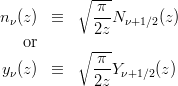
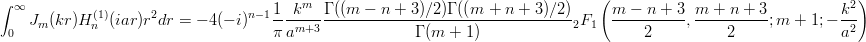
![\begin{eqnarray*}
\int_{0}^{\infty} j_1(kr)h_0^{(1)}(iar)r^3dr
&=& \int_{0}^{\infty} \frac{1}{k^2r^2}\left[ \sin(kr)-kr\cos(kr) \right] \left[ -\frac{e^{-ar}}{ar}\right]r^3dr \\
&=& -\frac{1}{ak^2}\int_{0}^{\infty} e^{-ar}\sin(kr)-kre^{-ar}\cos(kr) dr \\
&=& -\frac{1}{ak^2}\left[ \frac{k}{a^2+k^2}-k\frac{a^2-k^2}{(a^2+k^2)^2} \right] \\
&=& -\frac{2k}{a(a^2+k^2)^2}
\end{eqnarray*} \begin{eqnarray*}
\int_{0}^{\infty} j_1(kr)h_0^{(1)}(iar)r^3dr
&=& \int_{0}^{\infty} \frac{1}{k^2r^2}\left[ \sin(kr)-kr\cos(kr) \right] \left[ -\frac{e^{-ar}}{ar}\right]r^3dr \\
&=& -\frac{1}{ak^2}\int_{0}^{\infty} e^{-ar}\sin(kr)-kre^{-ar}\cos(kr) dr \\
&=& -\frac{1}{ak^2}\left[ \frac{k}{a^2+k^2}-k\frac{a^2-k^2}{(a^2+k^2)^2} \right] \\
&=& -\frac{2k}{a(a^2+k^2)^2}
\end{eqnarray*}](latex_a398712ff19b73a3b2750b4abb2b8cf83db367fb_p1.png)
![\begin{eqnarray*}
j_0(x) &=& \frac{1}{x}\sin(x) \\
j_1(x) &=& \frac{1}{x^2}\left[ \sin(x)-x\cos(x) \right] \\
j_2(x) &=& \frac{1}{x^3}\left[ (3-x^2)\sin(x)-3x\cos(x) \right] \\
j_3(x) &=& \frac{1}{x^4}\left[ (15-6x^2)\sin(x)-(15x-x^3)\cos(x) \right] \\
j_4(x) &=& \frac{1}{x^5}\left[ (105-45x^2+x^4)\sin(x)-(105x-10x^3)\cos(x) \right] \\
j_5(x) &=& \frac{1}{x^6}\left[ (945-420x^2+15x^4)\sin(x)-(945x-105x^3+x^5)\cos(x) \right] \\[2.0ex]
n_0(x) &=& y_0(x) = -\frac{1}{x}\cos(x) \\
n_1(x) &=& y_1(x) = -\frac{1}{x^2}\left[ \cos(x)+x\sin(x) \right] \\
n_2(x) &=& y_2(x) = -\frac{1}{x^3}\left[ (3-x^2)\cos(x)+3x\sin(x) \right] \\
n_3(x) &=& y_3(x) = -\frac{1}{x^4}\left[ (15-6x^2)\cos(x)+(15x-x^3)\sin(x) \right] \\
n_4(x) &=& y_4(x) = -\frac{1}{x^5}\left[ (105-45x^2+x^4)\cos(x)+(105x-10x^3)\sin(x) \right] \\
n_5(x) &=& y_5(x) = -\frac{1}{x^6}\left[ (945-420x^2+15x^4)\cos(x)+(945x-105x^3+x^5)\sin(x) \right] \\[2.0ex]
h^{(1)}_0(x) &=& -i\frac{e^{ix}}{x} \\
h^{(1)}_1(x) &=& -i\frac{e^{ix}}{x^2}(1-ix) \\
h^{(1)}_2(x) &=& -i\frac{e^{ix}}{x^3}(3-3ix-x^2) \\
h^{(1)}_3(x) &=& -i\frac{e^{ix}}{x^4}(15-15ix-6x^2+ix^3) \\
h^{(1)}_4(x) &=& -i\frac{e^{ix}}{x^5}(105-105ix-45x^2+10ix^3+x^4) \\
h^{(1)}_5(x) &=& -i\frac{e^{ix}}{x^6}(945-945ix-420x^2+105ix^3+15ix^4+x^5) \\[2.0ex]
h^{(1)}_0(ix) &=& -\frac{e^{-x}}{x} \\
h^{(1)}_1(ix) &=& i\frac{e^{-x}}{x^2}(1+x) \\
h^{(1)}_2(ix) &=& \frac{e^{-x}}{x^3}(3+3x+x^2) \\
h^{(1)}_3(ix) &=& -i\frac{e^{-x}}{x^4}(15+15x+6x^2+x^3) \\
h^{(1)}_4(ix) &=& -\frac{e^{-x}}{x^5}(105+105x+45x^2+10x^3+x^4) \\
h^{(1)}_5(ix) &=& i\frac{e^{-x}}{x^6}(945+945x+420x^2+105x^3+15x^4+x^5)
\end{eqnarray*} \begin{eqnarray*}
j_0(x) &=& \frac{1}{x}\sin(x) \\
j_1(x) &=& \frac{1}{x^2}\left[ \sin(x)-x\cos(x) \right] \\
j_2(x) &=& \frac{1}{x^3}\left[ (3-x^2)\sin(x)-3x\cos(x) \right] \\
j_3(x) &=& \frac{1}{x^4}\left[ (15-6x^2)\sin(x)-(15x-x^3)\cos(x) \right] \\
j_4(x) &=& \frac{1}{x^5}\left[ (105-45x^2+x^4)\sin(x)-(105x-10x^3)\cos(x) \right] \\
j_5(x) &=& \frac{1}{x^6}\left[ (945-420x^2+15x^4)\sin(x)-(945x-105x^3+x^5)\cos(x) \right] \\[2.0ex]
n_0(x) &=& y_0(x) = -\frac{1}{x}\cos(x) \\
n_1(x) &=& y_1(x) = -\frac{1}{x^2}\left[ \cos(x)+x\sin(x) \right] \\
n_2(x) &=& y_2(x) = -\frac{1}{x^3}\left[ (3-x^2)\cos(x)+3x\sin(x) \right] \\
n_3(x) &=& y_3(x) = -\frac{1}{x^4}\left[ (15-6x^2)\cos(x)+(15x-x^3)\sin(x) \right] \\
n_4(x) &=& y_4(x) = -\frac{1}{x^5}\left[ (105-45x^2+x^4)\cos(x)+(105x-10x^3)\sin(x) \right] \\
n_5(x) &=& y_5(x) = -\frac{1}{x^6}\left[ (945-420x^2+15x^4)\cos(x)+(945x-105x^3+x^5)\sin(x) \right] \\[2.0ex]
h^{(1)}_0(x) &=& -i\frac{e^{ix}}{x} \\
h^{(1)}_1(x) &=& -i\frac{e^{ix}}{x^2}(1-ix) \\
h^{(1)}_2(x) &=& -i\frac{e^{ix}}{x^3}(3-3ix-x^2) \\
h^{(1)}_3(x) &=& -i\frac{e^{ix}}{x^4}(15-15ix-6x^2+ix^3) \\
h^{(1)}_4(x) &=& -i\frac{e^{ix}}{x^5}(105-105ix-45x^2+10ix^3+x^4) \\
h^{(1)}_5(x) &=& -i\frac{e^{ix}}{x^6}(945-945ix-420x^2+105ix^3+15ix^4+x^5) \\[2.0ex]
h^{(1)}_0(ix) &=& -\frac{e^{-x}}{x} \\
h^{(1)}_1(ix) &=& i\frac{e^{-x}}{x^2}(1+x) \\
h^{(1)}_2(ix) &=& \frac{e^{-x}}{x^3}(3+3x+x^2) \\
h^{(1)}_3(ix) &=& -i\frac{e^{-x}}{x^4}(15+15x+6x^2+x^3) \\
h^{(1)}_4(ix) &=& -\frac{e^{-x}}{x^5}(105+105x+45x^2+10x^3+x^4) \\
h^{(1)}_5(ix) &=& i\frac{e^{-x}}{x^6}(945+945x+420x^2+105x^3+15x^4+x^5)
\end{eqnarray*}](latex_0b39f18e8d0e33d2ec0e57ce3b69cb8a49d7d313_p1.png)
![\begin{eqnarray*}
j_0(x) &=& \frac{1}{x}\sin(x) \\
j_1(x) &=& \frac{1}{x^2}\left[ \sin(x)-x\cos(x) \right] \\
j_2(x) &=& \frac{1}{x^3}\left[ (3-x^2)\sin(x)-3x\cos(x) \right] \\
j_3(x) &=& \frac{1}{x^4}\left[ (15-6x^2)\sin(x)-(15x-x^3)\cos(x) \right] \\
j_4(x) &=& \frac{1}{x^5}\left[ (105-45x^2+x^4)\sin(x)-(105x-10x^3)\cos(x) \right] \\
j_5(x) &=& \frac{1}{x^6}\left[ (945-420x^2+15x^4)\sin(x)-(945x-105x^3+x^5)\cos(x) \right] \\[2.0ex]
n_0(x) &=& y_0(x) = -\frac{1}{x}\cos(x) \\
n_1(x) &=& y_1(x) = -\frac{1}{x^2}\left[ \cos(x)+x\sin(x) \right] \\
n_2(x) &=& y_2(x) = -\frac{1}{x^3}\left[ (3-x^2)\cos(x)+3x\sin(x) \right] \\
n_3(x) &=& y_3(x) = -\frac{1}{x^4}\left[ (15-6x^2)\cos(x)+(15x-x^3)\sin(x) \right] \\
n_4(x) &=& y_4(x) = -\frac{1}{x^5}\left[ (105-45x^2+x^4)\cos(x)+(105x-10x^3)\sin(x) \right] \\
n_5(x) &=& y_5(x) = -\frac{1}{x^6}\left[ (945-420x^2+15x^4)\cos(x)+(945x-105x^3+x^5)\sin(x) \right] \\[2.0ex]
h^{(1)}_0(x) &=& -i\frac{e^{ix}}{x} \\
h^{(1)}_1(x) &=& -i\frac{e^{ix}}{x^2}(1-ix) \\
h^{(1)}_2(x) &=& -i\frac{e^{ix}}{x^3}(3-3ix-x^2) \\
h^{(1)}_3(x) &=& -i\frac{e^{ix}}{x^4}(15-15ix-6x^2+ix^3) \\
h^{(1)}_4(x) &=& -i\frac{e^{ix}}{x^5}(105-105ix-45x^2+10ix^3+x^4) \\
h^{(1)}_5(x) &=& -i\frac{e^{ix}}{x^6}(945-945ix-420x^2+105ix^3+15ix^4+x^5) \\[2.0ex]
h^{(1)}_0(ix) &=& -\frac{e^{-x}}{x} \\
h^{(1)}_1(ix) &=& i\frac{e^{-x}}{x^2}(1+x) \\
h^{(1)}_2(ix) &=& \frac{e^{-x}}{x^3}(3+3x+x^2) \\
h^{(1)}_3(ix) &=& -i\frac{e^{-x}}{x^4}(15+15x+6x^2+x^3) \\
h^{(1)}_4(ix) &=& -\frac{e^{-x}}{x^5}(105+105x+45x^2+10x^3+x^4) \\
h^{(1)}_5(ix) &=& i\frac{e^{-x}}{x^6}(945+945x+420x^2+105x^3+15x^4+x^5)
\end{eqnarray*} \begin{eqnarray*}
j_0(x) &=& \frac{1}{x}\sin(x) \\
j_1(x) &=& \frac{1}{x^2}\left[ \sin(x)-x\cos(x) \right] \\
j_2(x) &=& \frac{1}{x^3}\left[ (3-x^2)\sin(x)-3x\cos(x) \right] \\
j_3(x) &=& \frac{1}{x^4}\left[ (15-6x^2)\sin(x)-(15x-x^3)\cos(x) \right] \\
j_4(x) &=& \frac{1}{x^5}\left[ (105-45x^2+x^4)\sin(x)-(105x-10x^3)\cos(x) \right] \\
j_5(x) &=& \frac{1}{x^6}\left[ (945-420x^2+15x^4)\sin(x)-(945x-105x^3+x^5)\cos(x) \right] \\[2.0ex]
n_0(x) &=& y_0(x) = -\frac{1}{x}\cos(x) \\
n_1(x) &=& y_1(x) = -\frac{1}{x^2}\left[ \cos(x)+x\sin(x) \right] \\
n_2(x) &=& y_2(x) = -\frac{1}{x^3}\left[ (3-x^2)\cos(x)+3x\sin(x) \right] \\
n_3(x) &=& y_3(x) = -\frac{1}{x^4}\left[ (15-6x^2)\cos(x)+(15x-x^3)\sin(x) \right] \\
n_4(x) &=& y_4(x) = -\frac{1}{x^5}\left[ (105-45x^2+x^4)\cos(x)+(105x-10x^3)\sin(x) \right] \\
n_5(x) &=& y_5(x) = -\frac{1}{x^6}\left[ (945-420x^2+15x^4)\cos(x)+(945x-105x^3+x^5)\sin(x) \right] \\[2.0ex]
h^{(1)}_0(x) &=& -i\frac{e^{ix}}{x} \\
h^{(1)}_1(x) &=& -i\frac{e^{ix}}{x^2}(1-ix) \\
h^{(1)}_2(x) &=& -i\frac{e^{ix}}{x^3}(3-3ix-x^2) \\
h^{(1)}_3(x) &=& -i\frac{e^{ix}}{x^4}(15-15ix-6x^2+ix^3) \\
h^{(1)}_4(x) &=& -i\frac{e^{ix}}{x^5}(105-105ix-45x^2+10ix^3+x^4) \\
h^{(1)}_5(x) &=& -i\frac{e^{ix}}{x^6}(945-945ix-420x^2+105ix^3+15ix^4+x^5) \\[2.0ex]
h^{(1)}_0(ix) &=& -\frac{e^{-x}}{x} \\
h^{(1)}_1(ix) &=& i\frac{e^{-x}}{x^2}(1+x) \\
h^{(1)}_2(ix) &=& \frac{e^{-x}}{x^3}(3+3x+x^2) \\
h^{(1)}_3(ix) &=& -i\frac{e^{-x}}{x^4}(15+15x+6x^2+x^3) \\
h^{(1)}_4(ix) &=& -\frac{e^{-x}}{x^5}(105+105x+45x^2+10x^3+x^4) \\
h^{(1)}_5(ix) &=& i\frac{e^{-x}}{x^6}(945+945x+420x^2+105x^3+15x^4+x^5)
\end{eqnarray*}](latex_0b39f18e8d0e33d2ec0e57ce3b69cb8a49d7d313_p2.png)